Projects

  1. Projects
  2. Credit Card Transactions Data Analysis - How can Machine Learning Help with Fraud Detection? (Part 1)

Table of contents

  • Introduction
  • Project Summary
  • Data Collection and Metadata
  • Data preparation
  • Exploratory data analysis
  • Model Selection
  • Hyperparameter tuning of the XGBoost model

    • Introduction

    Credit card fraud comes in different forms; phishing, skimming and identity theft to name a few. This project focuses on developing a supervised machine learning model that will provide the best results in revealing and preventing fraudulent transactions. Part 1 of the project compares the accuracy of different machine learning models in classifying the credit card transaction data into valid and fraud transactions.

    Project Summary

    Part 1: Find the best predictive model among the common ML algorithms

    • Data collection and metadata
    • Data preparation
    • Model selection
    • Choosing the right performance metric
    • Train and evaluate the models
    • Comparing the model performances to find the winner model
    • Hypertuning the winner model's parameters
    • Comparing the winner model with the baseline model

    Part 2: Compare the accuracy of the winner of Part 1 with other algorithms that are specialized for rare-event analysis

    • Models for rare-event classification
      • SMOTE
      • Autoencoders
    • Train and evaluate the models
    • Compare the model performances and find the winner model
    • Make predictions
    • Conclusion

    Part 1

    Data Collection and Metadata

    About this data set:
    • The dataset contains transactions made by credit cards in September 2013 by European cardholders.
    • The dataset presents transactions that occurred in two days, where we have 492 fraud transactions among 284,807 transactions.
    • The dataset is extremely imbalanced with the positive class (frauds) account for only 0.172% of all transactions.
    • The dataset contains only numerical input variables which are the result of a PCA transformation.
    • Due to confidentiality, the original features and more background information about the data is not provided.
    • The dataset has 30 features, $\{V_1, V_2, ... V_{28}\}$ from PCA and two features which have not been transformed with PCA that are Time and Amount.
    • Time shows the time elapsed (in seconds) between each transaction and the first transaction in the dataset and Amount is the transaction amount.
    • Finally,Class is the response variable and it takes value 1 in case of fraud and 0 otherwise.
    Category Type Method
    1 Supervised Learning Classification Logistic Regression (LR)
    2 Support Vector Machines (SVM)
    3 K-Nearest Neighbours (KNN)
    4 Naive Bayes (NB)
    5 Artificial Neural Networks (ANN)
    6 Random Forests (RF)
    7 Decision Trees (DT)
    8 XGBoost (XGB)

    Data preparation

    Loading the libraries

    import warnings
import matplotlib
import numpy as np
import pandas as pd
import seaborn as sns
from collections import Counter
import matplotlib.pyplot as plt
from matplotlib import cm as cm
warnings.filterwarnings('ignore')
from IPython.display import Image
from matplotlib import rc, rcParams
from IPython.core.display import HTML
matplotlib.rcParams['font.family'] = 'serif'
rc('font',**{'family':'serif','serif':['Times']})
rc('text', usetex=False)
rc('text.latex', preamble=r'\usepackage{underscore}')
pd.set_option('display.float_format', lambda x: '%.2f' % x)
sns.set(rc={"figure.dpi":100})
sns.set_style('white')

    Loading data

    df = pd.read_csv("creditcard.csv")df.head()
    Time V1 V2 V3 V4 V5 V6 V7 V8 V9 ... V21 V22 V23 V24 V25 V26 V27 V28 Amount Class
    0 0.00 -1.36 -0.07 2.54 1.38 -0.34 0.46 0.24 0.10 0.36 ... -0.02 0.28 -0.11 0.07 0.13 -0.19 0.13 -0.02 149.62 0
    1 0.00 1.19 0.27 0.17 0.45 0.06 -0.08 -0.08 0.09 -0.26 ... -0.23 -0.64 0.10 -0.34 0.17 0.13 -0.01 0.01 2.69 0
    2 1.00 -1.36 -1.34 1.77 0.38 -0.50 1.80 0.79 0.25 -1.51 ... 0.25 0.77 0.91 -0.69 -0.33 -0.14 -0.06 -0.06 378.66 0
    3 1.00 -0.97 -0.19 1.79 -0.86 -0.01 1.25 0.24 0.38 -1.39 ... -0.11 0.01 -0.19 -1.18 0.65 -0.22 0.06 0.06 123.50 0
    4 2.00 -1.16 0.88 1.55 0.40 -0.41 0.10 0.59 -0.27 0.82 ... -0.01 0.80 -0.14 0.14 -0.21 0.50 0.22 0.22 69.99 0

    5 rows × 31 columns

    df.columns
    Index(['Time', 'V1', 'V2', 'V3', 'V4', 'V5', 'V6', 'V7', 'V8', 'V9', 'V10',
       'V11', 'V12', 'V13', 'V14', 'V15', 'V16', 'V17', 'V18', 'V19', 'V20',
       'V21', 'V22', 'V23', 'V24', 'V25', 'V26', 'V27', 'V28', 'Amount',
       'Class'],
       dtype='object')
    counter = Counter(df['Class'])
print(f'Class distribution of the response variable: {counter}')
print(f'Minority class corresponds to {100*counter[1]/(counter[0]+counter[1]):.3f}% of the data')
    Class distribution of the response variable: Counter({0: 284315, 1: 492})
Minority class corresponds to 0.173% of the data
    df.describe()
    Time V1 V2 V3 V4 V5 V6 V7 V8 V9 ... V21 V22 V23 V24 V25 V26 V27 V28 Amount Class
    count 284807.00 284807.00 284807.00 284807.00 284807.00 284807.00 284807.00 284807.00 284807.00 284807.00 ... 284807.00 284807.00 284807.00 284807.00 284807.00 284807.00 284807.00 284807.00 284807.00 284807.00
    mean 94813.86 0.00 0.00 -0.00 0.00 0.00 0.00 -0.00 0.00 -0.00 ... 0.00 -0.00 0.00 0.00 0.00 0.00 -0.00 -0.00 88.35 0.00
    std 47488.15 1.96 1.65 1.52 1.42 1.38 1.33 1.24 1.19 1.10 ... 0.73 0.73 0.62 0.61 0.52 0.48 0.40 0.33 250.12 0.04
    min 0.00 -56.41 -72.72 -48.33 -5.68 -113.74 -26.16 -43.56 -73.22 -13.43 ... -34.83 -10.93 -44.81 -2.84 -10.30 -2.60 -22.57 -15.43 0.00 0.00
    25% 54201.50 -0.92 -0.60 -0.89 -0.85 -0.69 -0.77 -0.55 -0.21 -0.64 ... -0.23 -0.54 -0.16 -0.35 -0.32 -0.33 -0.07 -0.05 5.60 0.00
    50% 84692.00 0.02 0.07 0.18 -0.02 -0.05 -0.27 0.04 0.02 -0.05 ... -0.03 0.01 -0.01 0.04 0.02 -0.05 0.00 0.01 22.00 0.00
    75% 139320.50 1.32 0.80 1.03 0.74 0.61 0.40 0.57 0.33 0.60 ... 0.19 0.53 0.15 0.44 0.35 0.24 0.09 0.08 77.16 0.00
    max 172792.00 2.45 22.06 9.38 16.88 34.80 73.30 120.59 20.01 15.59 ... 27.20 10.50 22.53 4.58 7.52 3.52 31.61 33.85 25691.16 1.00

    8 rows × 31 columns

    Normalizing the features

    I use Re-scaling (min-max normalization) to normalize the features. Re-scaling transforms all the numerical features to the range $[-1,\,1]$

    $$ \text{min-max normalization: }x \rightarrow -1 + \frac{2(x-min(x))}{max(x)-min(x)} $$ 
    df.iloc[:,:30] = -1 + (df.iloc[:,:30] - df.iloc[:,:30].min())*2 / (df.iloc[:,:30].max() - df.iloc[:,:30].min())
    df.describe()
    Time V1 V2 V3 V4 V5 V6 V7 V8 V9 ... V21 V22 V23 V24 V25 V26 V27 V28 Amount Class
    count 284807.00 284807.00 284807.00 284807.00 284807.00 284807.00 284807.00 284807.00 284807.00 284807.00 ... 284807.00 284807.00 284807.00 284807.00 284807.00 284807.00 284807.00 284807.00 284807.00 284807.00
    mean 0.10 0.92 0.53 0.67 -0.50 0.53 -0.47 -0.47 0.57 -0.07 ... 0.12 0.02 0.33 -0.24 0.16 -0.15 -0.17 -0.37 -0.99 0.00
    std 0.55 0.07 0.03 0.05 0.13 0.02 0.03 0.02 0.03 0.08 ... 0.02 0.07 0.02 0.16 0.06 0.16 0.01 0.01 0.02 0.04
    min -1.00 -1.00 -1.00 -1.00 -1.00 -1.00 -1.00 -1.00 -1.00 -1.00 ... -1.00 -1.00 -1.00 -1.00 -1.00 -1.00 -1.00 -1.00 -1.00 0.00
    25% -0.37 0.89 0.52 0.64 -0.57 0.52 -0.49 -0.48 0.57 -0.12 ... 0.12 -0.03 0.33 -0.33 0.12 -0.26 -0.17 -0.38 -1.00 0.00
    50% -0.02 0.92 0.54 0.68 -0.50 0.53 -0.48 -0.47 0.57 -0.08 ... 0.12 0.02 0.33 -0.22 0.16 -0.17 -0.17 -0.37 -1.00 0.00
    75% 0.61 0.96 0.55 0.71 -0.43 0.54 -0.47 -0.46 0.58 -0.03 ... 0.13 0.07 0.34 -0.12 0.20 -0.07 -0.16 -0.37 -0.99 0.00
    max 1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00 ... 1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00

    8 rows × 31 columns

    Exploratory data analysis

    Correlation plot

    fig, ax = plt.subplots(1, 1, figsize=(14,14))
corr = df.corr()
ax_ = sns.heatmap(
    corr, 
    vmin=-1, vmax=1, center=0,
    cmap=sns.diverging_palette(20, 220, n=200),
    square=True,
    ax=ax,
    cbar_kws={'shrink': 0.82}
)
ax_.set_xticklabels(
    ax.get_xticklabels(),
    rotation=45,
    horizontalalignment='right'
)
ax.set_title('Correlation between principal components of the credit card dataset', fontsize=18, y=1.02);

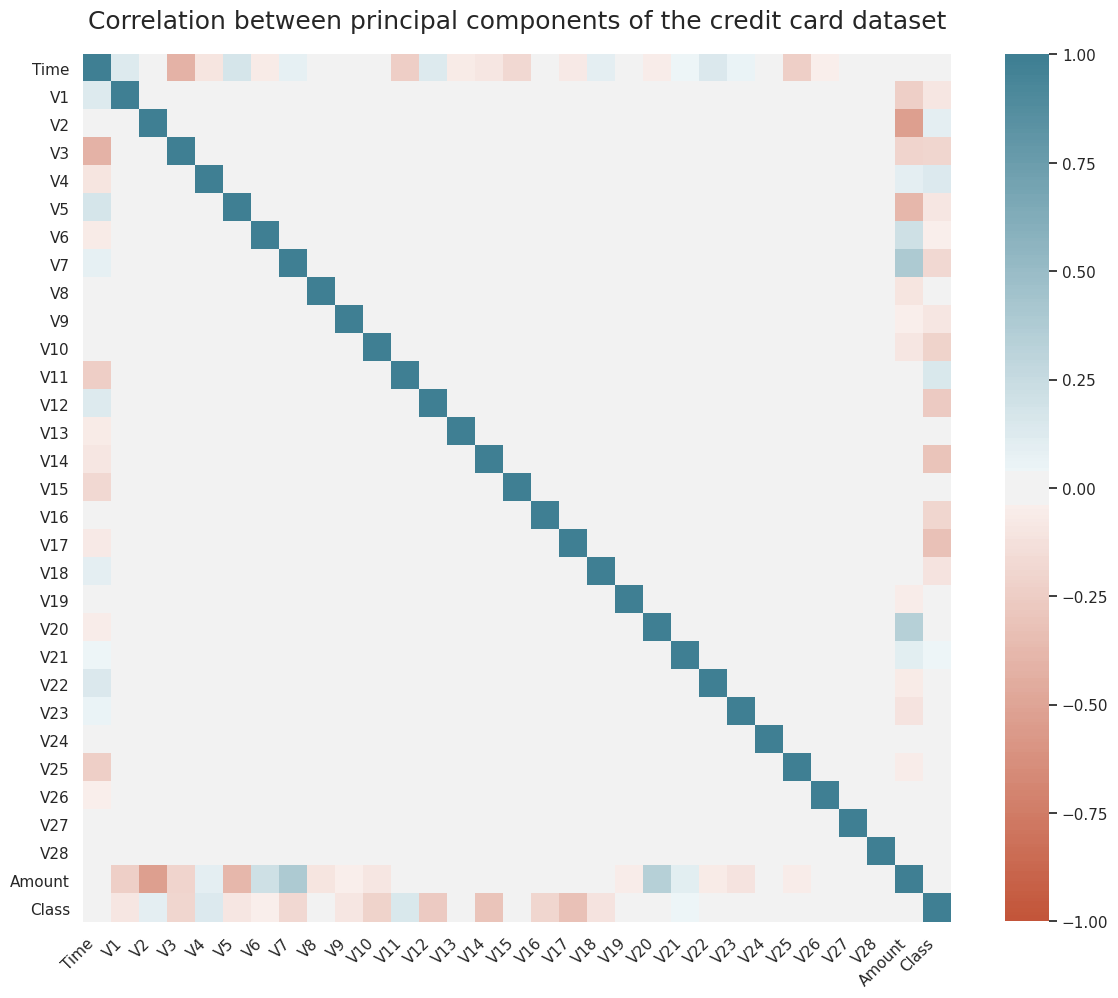
    As we can see in Figure 1, most of the data features are not correlated. This is because before publishing, most of the features have been transformed using Principal Component Analysis (PCA). The importance of these features, however, could be assessed using the RandomForestClassifier.feature_importances_ of sklearn.ensemble which requires training a classification tree on the data or SelectKbest method from sklearn.feature_selection for a general model.

    Feature importance

    from sklearn.ensemble import RandomForestClassifier
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import f_classif

def get_feature_importance_Kbest(X, y, feature_names, n_features_to_plot=30):
    kbest = SelectKBest(score_func=f_classif, k=n_features_to_plot)
    fit = kbest.fit(X, y)
    feature_ids_sorted = np.argsort(fit.scores_)[::-1]
    features_sorted_by_importance = np.array(feature_names)[feature_ids_sorted]
    try:
        feature_importance_array = np.vstack((
        features_sorted_by_importance[:n_features_to_plot], 
        np.array(sorted(fit.scores_)[::-1][:n_features_to_plot])
    )).T
    except:
        feature_importance_array = np.vstack((
        features_sorted_by_importance[:], 
        np.array(sorted(fit.scores_)[::-1][:])
    )).T
            
    feature_importance_data = pd.DataFrame(feature_importance_array, columns=['feature', 'score'])
    feature_importance_data['score'] = feature_importance_data['score'].astype(float)
    return feature_importance_data

# Using RF feature_importances_
def get_feature_importance_RF(X, y, feature_names, n_features_to_plot=30):
    RF = RandomForestClassifier(random_state=0)
    RF.fit(X, y)
    importances_RF = RF.feature_importances_
    feature_ids_sorted = np.argsort(importances_RF)[::-1]
    features_sorted_by_importance = np.array(feature_names)[feature_ids_sorted]
    try:
        feature_importance_array = np.vstack((
        features_sorted_by_importance[:n_features_to_plot], 
        np.array(sorted(importances_RF)[::-1][:n_features_to_plot])
    )).T
    except:
        feature_importance_array = np.vstack((
        features_sorted_by_importance[:], 
        np.array(sorted(importances_RF)[::-1][:])
    )).T
    feature_importance_data = pd.DataFrame(feature_importance_array, columns=['feature', 'score'])
    feature_importance_data['score'] = feature_importance_data['score'].astype(float)
    return feature_importance_data

# Features and response variable
X = df.iloc[:,:30].values
y = df.iloc[:,30].values
feature_names = list(df.columns.values[:30])

# Using KBest
importances_KBest = get_feature_importance_Kbest(X, y, feature_names)

# Using RF
importances_RF = get_feature_importance_RF(X, y, feature_names)
    pd.concat([importances_RF,importances_KBest],axis=1)
    RF KBest
    feature score feature score
    0 V14 0.14 V17 33979.17
    1 V17 0.14 V14 28695.55
    2 V12 0.13 V12 20749.82
    3 V10 0.09 V10 14057.98
    4 V16 0.08 V16 11443.35
    5 V11 0.06 V3 11014.51
    6 V9 0.04 V7 10349.61
    7 V18 0.03 V11 6999.36
    8 V7 0.02 V4 5163.83
    9 V4 0.02 V18 3584.38
    10 V26 0.02 V1 2955.67
    11 V21 0.02 V9 2746.60
    12 V1 0.01 V5 2592.36
    13 V6 0.01 V2 2393.40
    14 V3 0.01 V6 543.51
    15 V8 0.01 V21 465.92
    16 Time 0.01 V19 344.99
    17 V5 0.01 V20 115.00
    18 V2 0.01 V8 112.55
    19 V20 0.01 V27 88.05
    20 V19 0.01 Time 43.25
    21 V27 0.01 V28 25.90
    22 V22 0.01 V24 14.85
    23 Amount 0.01 Amount 9.03
    24 V13 0.01 V13 5.95
    25 V15 0.01 V26 5.65
    26 V24 0.01 V15 5.08
    27 V28 0.01 V25 3.12
    28 V25 0.01 V23 2.05
    29 V23 0.01 V22 0.18

    Note that the two methods rank the features similarly in terms of importance.

    Class distributions for the 5 most important fatures

    cols = ["#009900", "#ffcc00", "#0099cc", "#cc0066", "#666699"]
fig = plt.figure(figsize=(8,8), dpi=100)
important_features = ['V14','V17','V12','V10','V16']
theta=2*np.pi/5
offset = np.pi/2 - theta
radius = 0.3
pentagon_vertices = [[0.5+radius*(np.cos(x*theta+offset)), 
                      0.5+radius*(np.sin(x*theta+offset))] 
                     for x in range(5)]
for i, col in enumerate(important_features):
    tmp_ax =fig.add_axes([pentagon_vertices[i][0],
                          pentagon_vertices[i][1],
                          .25,
                          .25])
    sns.kdeplot(df[df['Class']==0][col], shade=True, color=cols[i], ax=tmp_ax)
    sns.kdeplot(df[df['Class']==1][col], shade=False, color=cols[i], ax=tmp_ax, linestyle="--")
    tmp_ax.set_xticklabels([])
    tmp_ax.set_yticklabels([])
    tmp_ax.set_title(important_features[i], fontsize=14)
    if i==len(important_features)-1:
        leg = tmp_ax.get_legend()
        leg.legendHandles[0].set_color('k')
        leg.legendHandles[1].set_color('k')
    plt.legend([], [], frameon=False)
fig.legend(leg.legendHandles, ['valid','fraud'], loc='center')
sns.despine(left=True)
plt.suptitle('Kernel Density Estimate (KDE) plot of class distributions for \n 5 most important features', x=0.64, y=1.15);

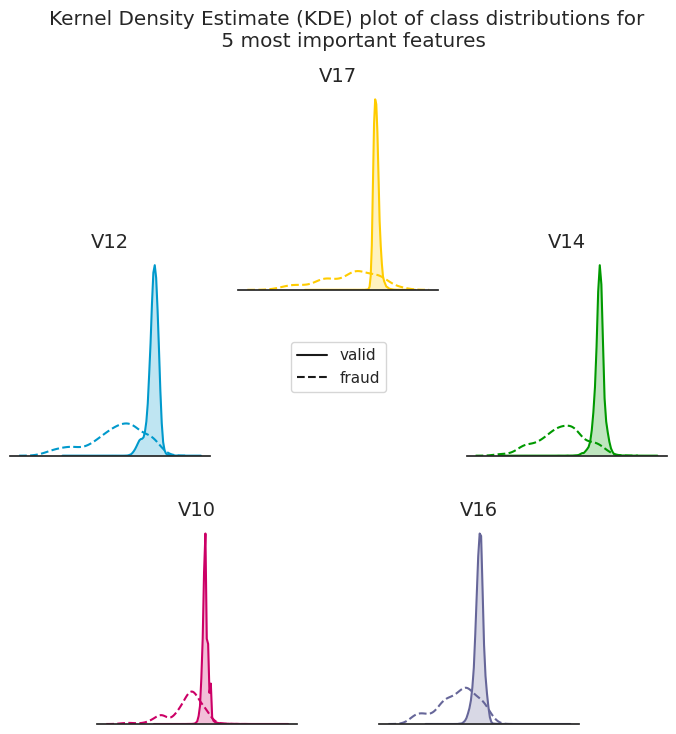
    Model Selection

    This part explains the model selection process. We use the sklearn implementation of the candidate models except for the XGBoost classifier where we use the xgboost library.

    Notes regarding the model selection process

    • Due to the extreme class imbalance in the dataset, we take advantage of the sklearn's Stratified K-Folds cross-validator (StratifiedKFold) to ensure that the observations are distributed with a similar class ratio $\bigg(\dfrac{\text{positive class count}}{\text{negative class count}}\bigg)$ across the folds.
    • We choose scoring='average_precision' as the model evaluation criteria. Ideally we'd want to use Precision-Recall Area Under Curve (PR-AUC) as the criteria but since it is not provided by sklearn, we use average_precision (AP) which summarizes a precision-recall curve as the weighted mean of precisions achieved at each threshold, with the increase in recall from the previous threshold used as the weight:
      • $$ \text{AP} = \sum_n (R_n - R_{n-1}) P_n, $$

      where $P_n$ and $R_n$ are the precision and recall, respectively, at the $n$-th threshold [ref]. 

    # A whole host of Scikit-learn models
from sklearn.svm import SVC
from sklearn.naive_bayes import GaussianNB
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.tree import DecisionTreeClassifier
from xgboost import XGBClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.pipeline import make_pipeline
from sklearn.model_selection import train_test_split
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import StratifiedKFold
import time

# We use StratifiedKFold to guarantee similar distribution in train and test data
# We set the train:test ratio to 4:1 - The train set will ultimately be split
# into train and validation sets itself, with the same ratio! See below

#              X
#  ___________/\___________
# /                        \
#  x_1, x_2, x_3, ... , x_n

#       X_train       X_test
#  _______/\_______   __/\__
# /                \ /     \

# X_test will be unseen until the very last step!

#       X_train     
#  _______/\_______ 
# /                \
#         ||
#         ||
#         \/
#
#     X_tr     X_val 
#  ____/\____  _/\_ 
# /          \/    \ 

num_splits = 5
skf = StratifiedKFold(n_splits=num_splits, random_state=1, shuffle=True)

# Features and response variable
X = df.iloc[:,:30].values
y = df.iloc[:,30].values

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=1, stratify=y)

model_dict = {'CT':[DecisionTreeClassifier()], 
              'GB':[GradientBoostingClassifier()], 
              'KNN':[KNeighborsClassifier()],
              'LR':[LogisticRegression()], 
              'NB':[GaussianNB()], 
              'RF':[RandomForestClassifier()], 
              'SVC':[SVC()], 
              'XGB':[XGBClassifier()]}

    Comparing the model performances to find the winner model

    for model_name, model in model_dict.items():
                  
    # train the model
    t_start = time.time()
    cv_results = cross_val_score(model[0], 
                                 X_train, 
                                 y_train, 
                                 cv=skf, 
                                 scoring='average_precision', 
                                 verbose=10, 
                                 n_jobs=-1) 
    
    # save the results
    calc_time = time.time() - t_start
    model_dict[model_name].append(cv_results)
    model_dict[model_name].append(calc_time)
    print(("{0} model gives an AP of {1:.2f}% with a standard deviation "
           "{2:.2f} (took {3:.1f} seconds)").format(model_name, 
                                                    100*cv_results.mean(), 
                                                    100*cv_results.std(), 
                                                    calc_time)
         )
            [Parallel(n_jobs=-1)]: Using backend LokyBackend with 24 concurrent workers.
        [Parallel(n_jobs=-1)]: Done   2 out of   5 | elapsed:   15.6s remaining:   23.4s
        [Parallel(n_jobs=-1)]: Done   3 out of   5 | elapsed:   15.8s remaining:   10.5s
        [Parallel(n_jobs=-1)]: Done   5 out of   5 | elapsed:   16.9s remaining:    0.0s
        [Parallel(n_jobs=-1)]: Done   5 out of   5 | elapsed:   16.9s finished
        [Parallel(n_jobs=-1)]: Using backend LokyBackend with 24 concurrent workers.
    
        CT model gives an AP of 53.17% with a standard deviation 3.44 (took 17.1 seconds)
    
        [Parallel(n_jobs=-1)]: Done   2 out of   5 | elapsed:  4.6min remaining:  6.9min
        [Parallel(n_jobs=-1)]: Done   3 out of   5 | elapsed:  4.6min remaining:  3.1min
        [Parallel(n_jobs=-1)]: Done   5 out of   5 | elapsed:  4.7min remaining:    0.0s
        [Parallel(n_jobs=-1)]: Done   5 out of   5 | elapsed:  4.7min finished
        [Parallel(n_jobs=-1)]: Using backend LokyBackend with 24 concurrent workers.
    
        GB model gives an AP of 59.87% with a standard deviation 4.48 (took 279.6 seconds)
    
        [Parallel(n_jobs=-1)]: Done   2 out of   5 | elapsed:  1.8min remaining:  2.7min
        [Parallel(n_jobs=-1)]: Done   3 out of   5 | elapsed:  2.0min remaining:  1.3min
    
        KNN model gives an AP of 78.70% with a standard deviation 3.31 (took 131.1 seconds)
    
        [Parallel(n_jobs=-1)]: Done   5 out of   5 | elapsed:  2.2min remaining:    0.0s
        [Parallel(n_jobs=-1)]: Done   5 out of   5 | elapsed:  2.2min finished
        [Parallel(n_jobs=-1)]: Using backend LokyBackend with 24 concurrent workers.
        [Parallel(n_jobs=-1)]: Done   2 out of   5 | elapsed:    2.9s remaining:    4.3s
        [Parallel(n_jobs=-1)]: Done   3 out of   5 | elapsed:    2.9s remaining:    1.9s
        [Parallel(n_jobs=-1)]: Done   5 out of   5 | elapsed:    3.1s remaining:    0.0s
        [Parallel(n_jobs=-1)]: Done   5 out of   5 | elapsed:    3.1s finished
        [Parallel(n_jobs=-1)]: Using backend LokyBackend with 24 concurrent workers.
    
        LR model gives an AP of 72.42% with a standard deviation 2.56 (took 3.3 seconds)
    
        [Parallel(n_jobs=-1)]: Done   2 out of   5 | elapsed:    0.5s remaining:    0.8s
        [Parallel(n_jobs=-1)]: Done   3 out of   5 | elapsed:    0.5s remaining:    0.4s
        [Parallel(n_jobs=-1)]: Done   5 out of   5 | elapsed:    0.5s remaining:    0.0s
        [Parallel(n_jobs=-1)]: Done   5 out of   5 | elapsed:    0.5s finished
        [Parallel(n_jobs=-1)]: Using backend LokyBackend with 24 concurrent workers.
    
        NB model gives an AP of 8.54% with a standard deviation 0.50 (took 0.7 seconds)
    
        [Parallel(n_jobs=-1)]: Done   2 out of   5 | elapsed:  2.7min remaining:  4.0min
        [Parallel(n_jobs=-1)]: Done   3 out of   5 | elapsed:  2.7min remaining:  1.8min
        [Parallel(n_jobs=-1)]: Done   5 out of   5 | elapsed:  3.0min remaining:    0.0s
        [Parallel(n_jobs=-1)]: Done   5 out of   5 | elapsed:  3.0min finished
        [Parallel(n_jobs=-1)]: Using backend LokyBackend with 24 concurrent workers.
    
        RF model gives an AP of 84.02% with a standard deviation 3.00 (took 180.4 seconds)
    
        [Parallel(n_jobs=-1)]: Done   2 out of   5 | elapsed:   10.4s remaining:   15.6s
        [Parallel(n_jobs=-1)]: Done   3 out of   5 | elapsed:   10.5s remaining:    7.0s
        [Parallel(n_jobs=-1)]: Done   5 out of   5 | elapsed:   10.7s remaining:    0.0s
        [Parallel(n_jobs=-1)]: Done   5 out of   5 | elapsed:   10.7s finished
        [Parallel(n_jobs=-1)]: Using backend LokyBackend with 24 concurrent workers.
    
        SVC model gives an AP of 75.22% with a standard deviation 3.54 (took 10.8 seconds)
    
        [Parallel(n_jobs=-1)]: Done   2 out of   5 | elapsed:  1.6min remaining:  2.4min
        [Parallel(n_jobs=-1)]: Done   3 out of   5 | elapsed:  1.6min remaining:  1.1min
    
        XGB model gives an AP of 84.89% with a standard deviation 2.92 (took 98.1 seconds)
    
        [Parallel(n_jobs=-1)]: Done   5 out of   5 | elapsed:  1.6min remaining:    0.0s
        [Parallel(n_jobs=-1)]: Done   5 out of   5 | elapsed:  1.6min finished

    XGB and RF outperform the other algorithms with XGB being slightly more accurate than the random forest classifier so as we said previously, we choose XGB as the winner. In the next part, we will go through the process of tuning the model.

    Hyperparameter tuning of the XGBoost model

    In this part, we'd like to find the set of model parameters that work best on our credit card fraud detection problem. How can we configure the model so that we get the best model performance for the dataset we have and the evaluation metric that we specify?

    We are aiming to achieve this while ensuring that the resulted parameters don't cause overfitting. We use XGBClassifier() with the default parameters as the baseline classifier. The following describes a summary of the steps and some important notes regarding the model parameters and cross-validation methodology:

    • We split the data into training and test splits while maintaining the class ratio (exactly what we did in the model selection)
    • Model performance on the test data (X_test, y_test) is not going to be assessed until the final model evaluation where both the baseline classifier and the tuned model are going to be tested against the unseen test data
    • We use RepeatedStratifiedKFold() which repeats the StratifiedKFold() $n_{\mathrm{repeats}}$ times ($3\leq n_{\mathrm{repeats}} \leq 10$) and outputs the model performance-metric (PR-AUC in this case) as the mean across all folds and all repeats. This improves the estimate of the mean model performance-metric with the downside of increased model-evaluation cost. We use $n_{\mathrm{repeats}}=5$ in this work.
    • early stopping is one way to reduce overfitting of training data. Here's a brief summary of how it works:
      • The user specifies an evaluation metric (eval_metric) and a validation set (eval_set) to be monitored during the training process.
      • The evaluation metric for the eval_set needs to "improve" at least once every early_stopping_rounds of boosting rounds so that the training continues.
      • Early stopping terminates the training process when the number of boosting rounds with no improvement in evaluation-metric for the eval_set reaches early_stopping_rounds.
      • XGBoost offers a wide range of evaluation metrics (see here for the full list) that are either minimized (RMSE, log loss, etc.) or maximized (MAP, NDCG, AUC) during the training process. We use aucpr for this classification problem for the reasons discussed earlier.
    • Normally, we would use sklearn`s GridsearchCV() to find the hyperparameters of the model. This works great, especially if the model is a native sklearn model. Infact, most sklearn models come with their CV version, e.g., LogisticRegressionCV(), which performs grid search over the user-defined hyperparameter dictionary. However, as we mentioned, when we try to use XGBoost's early stopping, we need to specify an eval_set to compare the evaluation-metric performance on it with that of the training data. Now if we use GridSearchCV(), ideally we would want XGBoost to use the held-out fold as the evaluation set to determine the optimal number of boosting rounds, however, that doesn't seem to be possible when using GridSearchCV(). One way is to use a static held-out set for XGBoost but that doesn't make sense as it defeats the purpose of cross validation. To address this issue, I defined a custom cross-validation function that for each hyperparameter-set candidate:
      1. For each fold, finds the optimal number of boosting rounds, the number of rounds where the eval_metric reached its best value (best_score) for the eval_set.
      2. Reports the mean and standard deviation of the eval_metric (for both training and evaluation data) and best number of rounds by averaging over the folds.
      3. Finally, returns the optimal combination of hyperparameters that gave the best eval_metric.
    • Note: xgboost.best_ntree_limit you do best_nrounds = int(best_nrounds / 0.8) you consider that your validation set was 20% of your whole training data (another way of saying that you performed a 5-fold cross-validation). The rule can then be generalized as: n_folds = 5 best_nrounds = int((res.shape[0] - estop) / (1 - 1 / n_folds))
    • Because XGBClassifier() accepts a lot of hyperparameters, it would be computationally inefficient and extremely time-consuming to iterate over the enormous number of hyperparameter combinations. What we can do instead is to divide the parameters into a few independent or weakly-interacting groups and find the best hyperparameter combination for each group. The optimal set of parameters can ultimately be determined as the union of the best hyperparameter groups. The following is the hyperparameter groups and the order that we optimize them (reference):
      1. max_depth, min_child_weight
      2. colsample_bytree, colsample_bylevel, subsample
      3. alpha, gamma
      4. scale_pos_weight
      5. learning_rate
    • To ensure that the model hyperparameters don't cause overfitting, we save the model's eval_metric results for both training and validation data. At the end, we throw out the set of hyperparameters where the model exhibits a better performance for the training data than the validation data.
    • Because we are using early stopping, the model throws out the optimal number of trees (n_estimators) for each fold. For each parameter group, the best number of boosting trees is returned as the mean over the folds.
    • We use a Python dictionary, progress, to record the changes in validation and training data eval_metric(s). This can help a lot with assessing whether the model is overfitting or not.
    • Our efforts to reduce overfitting are in accordance with XGBoost's Notes on Parameter Tuning.

    Data preparation for CV

    import xgboost as xgb
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.model_selection import train_test_split

# load data
X = df.iloc[:,:30].values
y = df.iloc[:,30].values
all_features = list(df.columns.values[:30])

# train-test stratified split; stratify=y is used to ensure
# that the two splits have similar class distribution
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=1, stratify=y)

model = XGBClassifier(tree_method='gpu_hist', 
                      objective='binary:logistic')
    
# fold parameters
num_splits = 4
num_reps = 5
rand_state = 123
rskf = RepeatedStratifiedKFold(n_splits=num_splits,
                               n_repeats=num_reps, 
                               random_state=rand_state)

    Helper functions for CV

    First, we define a function that for the given set of hyperparameters, trains the XGBClassifier() and spits out the model's mean-over-folds performance metrics.

    from sklearn.metrics import average_precision_score
from datetime import datetime, timedelta
from itertools import product
from pprint import pprint
np.set_printoptions(threshold=5)

Early_Stop_Rounds = 400
Num_Boosting_Rounds = 4000

from sklearn.metrics import average_precision_score
from datetime import datetime, timedelta
from itertools import product
from pprint import pprint
import random
np.set_printoptions(threshold=5)

Early_Stop_Rounds = 400
Num_Boosting_Rounds = 4000

def cv_summary(X_data, y_data, params, feature_names, cv, 
               objective_func='binary:logistic', 
               eval_metric='aucpr', 
               spit_out_fold_results=False, 
               spit_out_summary=True, 
               num_boost_rounds=Num_Boosting_Rounds, 
               early_stop_rounds=Early_Stop_Rounds, 
               save_fold_preds=False):
    """
    Returns cv results for a given set of parameters
    """
    
    # number of folds
    num_splits = cv.cvargs['n_splits']
    # num_rounds: total number of rounds (= n_repeats*n_folds)
    num_rounds = cv.get_n_splits()
    
    # train_scores and val_scores store the mean over all repeats of 
    # the in-sample and held-out predictions, respectively
    train_scores = np.zeros(num_rounds)
    valid_scores = np.zeros(num_rounds)
    best_num_estimators = np.zeros(num_rounds)
    
    # track eval results
    eval_results = []
    fold_preds = {'train':[], 'eval':[]}
        
    for i, (train_index, valid_index) in enumerate(cv.split(X_data, y_data)):
        
        # which repeat
        rep = i//num_splits + 1 
        
        # which fold
        fold = i%num_splits + 1
        
        # XGBoost train uses DMatrix 
        xg_train = xgb.DMatrix(X_data[train_index,:], 
                               feature_names=feature_names, 
                               label = y_data[train_index])
        
        xg_valid = xgb.DMatrix(X_data[valid_index,:], 
                               feature_names=feature_names, 
                               label = y_data[valid_index])   
        # set evaluation 
        params['tree_method'] = 'gpu_hist'
        params['objective'] = objective_func
        params['eval_metric'] = eval_metric
        
        # track eval results
        progress = dict()
        
        # train using train data
        if early_stop_rounds is not None:
            clf = xgb.train(params, xg_train, 
                            num_boost_round = num_boost_rounds, 
                            evals=[(xg_train, "train"), (xg_valid, "eval")], 
                            early_stopping_rounds=early_stop_rounds, 
                            evals_result=progress, 
                            verbose_eval=False)
            
            # for validation data we don't need to set ntree_limit because from
            # XGBoost docs:
            #
            # fit():
            #
            # if early_stopping_rounds is not None:
            #     self.best_ntree_limit = self._Booster.best_ntree_limit
            # ...
            # ...
            # predict():
            #
            # if ntree_limit is None:
            #     ntree_limit = getattr(self, "best_ntree_limit", 0)
            
            y_pred_vl = clf.predict(xgb.DMatrix(X_train[valid_index,:], 
                                                feature_names=feature_names))
            
            # for train data, we scale up the number of rounds, i.e., we consider that the 
            # validation set size was 1/num_splits of the training data size. Essentially
            # what we report as the optimal number of boosting trees is for a data with 
            # the size of the training data
            
            best_num_estimators[i] = int(clf.best_ntree_limit / (1 - 1 / num_splits))
#           clf.setattr("best_ntree_limit", best_num_estimators[i])
            
            y_pred_tr = clf.predict(xgb.DMatrix(X_train[train_index,:], 
                                                feature_names=feature_names))
            
            
        else:
            clf = xgb.train(params, xg_train, 
                            num_boost_round = num_boost_rounds, 
                            evals=[(xg_train, "train"), (xg_valid, "eval")], 
                            verbose_eval=False, 
                            evals_result=progress)     
            best_num_estimators[i] = num_boost_rounds
            y_pred_tr = clf.predict(xgb.DMatrix(X_train[train_index,:], 
                                                feature_names=feature_names),  
                                                ntree_limit=0)
            y_pred_vl = clf.predict(xgb.DMatrix(X_train[valid_index,:], 
                                                feature_names=feature_names), 
                                                ntree_limit=0)
        
        train_scores[i] = average_precision_score(y_train[train_index], y_pred_tr)
        valid_scores[i] = average_precision_score(y_train[valid_index], y_pred_vl)
        
        if save_fold_preds:
            fold_preds['train'].append([y_train[train_index], y_pred_tr])
            fold_preds['eval'].append([y_train[valid_index], y_pred_vl])

        
        if spit_out_fold_results:
            
            print(f"\n Repeat {rep}, Fold {fold} -", 
                  f"PR-AUC tr = {train_scores[i]:<.3f},", 
                  f"PR-AUC vl = {valid_scores[i]:<.3f}",
                  f"(diff = {train_scores[i] - valid_scores[i]:<.4f})",
                  )
            if early_stop_rounds is not None:
                print(f" best number of boosting rounds tr = {best_num_estimators[i]:<.0f}")
                
        eval_results.append(progress)
        
    # End of each repeat
    if spit_out_summary:
        
        print(f"\nSummary:\n", 
              f"mean PR-AUC training =  {np.average(train_scores):<.3f}\n",
              f"mean PR-AUC validation = {np.average(valid_scores):<.3f}\n",
              f"mean PR-AUC difference = {np.average(train_scores-valid_scores):<.4f}"
             )
        if early_stop_rounds is not None:
            print(f" average number of boosting rounds tr = {np.average(best_num_estimators):<.0f}")
    out = [(np.average(x), np.std(x)) for x in [train_scores, valid_scores, best_num_estimators]]
    return out, eval_results, fold_preds, clf
    
def cv_search_params(X_data, y_data, param_dict, feature_names, cv, 
                     objective_func='binary:logistic', eval_metric='aucpr', 
                     spit_out_fold_results=False, spit_out_summary=True, 
                     num_boost_rounds=Num_Boosting_Rounds, 
                     early_stop_rounds=None, random_grid_search = False, 
                     save_fold_preds=False,
                     num_random_search_candidates=10):
    """
    Returns the cv_summary() for all the combinations of the given parameter dictionary
    """
    
    search_results = []
    param_values = [
        x if (isinstance(x, list) or isinstance(x, type(np.linspace(1,2,2))))
          else [x] for x in param_dict.values()
                 ]
    param_dict = dict(zip(tuple(param_dict.keys()), param_values))
    num_search_candidates = len(list(product(*param_values)))
    all_search_params = []
    num_rand_search_candidates = num_random_search_candidates
    random_sample_ids = random.sample(range(num_search_candidates), num_rand_search_candidates)
    all_search_params = []
    for i, search_params in enumerate(product(*param_values)):
        current_params = dict(zip(tuple(param_dict.keys()), search_params))
        all_search_params.append(current_params)
    if random_grid_search:
        all_search_params = list(np.array(all_search_params)[random_sample_ids])
    evals = [[] for i in range(len(all_search_params))]
    print(f"Grid search started at {datetime.now()}")   
    print(f"Total number of hyperparameter candidates = {len(evals)}")     
    for i, search_params in enumerate(all_search_params):
        start_time = datetime.now()
        current_params = search_params
        print(f'\nCV {i+1} on:\n')
        pprint({k: v for k, v in current_params.items() if len(param_dict[k])>1})
        print('\n started!')
        results, evals[i], _, _ = cv_summary(X_data, y_data, 
                                             current_params, feature_names, 
                                             cv, objective_func=objective_func, 
                                             eval_metric=eval_metric, 
                                             spit_out_fold_results=spit_out_fold_results, 
                                             spit_out_summary=spit_out_summary, 
                                             early_stop_rounds=early_stop_rounds, 
                                             num_boost_rounds=num_boost_rounds)
        end_time = datetime.now()
        time_taken = f"{(end_time-start_time).total_seconds():.2f}"
        if len(evals)>1:
            print(f'CV {i+1} ended! (took {time_taken} seconds)')
        else:
            print(f'CV ended! (took {time_taken} seconds)')
        [(tr_avg, tr_std), 
        (val_avg, val_std), 
        (numtrees_avg, numtrees_std)] = results
        search_results.append([current_params, 
                               tr_avg, tr_std, 
                               val_avg, val_std, 
                               numtrees_avg, numtrees_std, 
                               tr_avg-val_avg, time_taken])
        
    print(f"Grid search ended at {datetime.now()}")  
    search_df = pd.DataFrame(search_results, 
                             columns=['current_params', 'tr_avg', 'tr_std', 
                                      'val_avg', 'val_std', 'numtrees_avg', 
                                      'numtrees_std', 'diff', 'time_taken'])
    
    return search_df, evals

    Dividing the hyperparameters into orthogonal groups

    Next, we define a hyperparameter dictionary and update it with some initial parameters for the model: 

    cur_params = {
    'max_depth': 3,
    'min_child_weight': 5,
    'subsample': 1,
    'colsample_bytree': 1,
    'colsample_bylevel': 1,
    'alpha': 1,
    'gamma': 1,
    'scale_pos_weight': 1,
    'learning_rate': 2e-3,
}

    We then define the parameter groups that are going to be the target of grid search: 

    # current xgb parameters
param_group_1 = {'max_depth': [3, 4], 'min_child_weight': [1, 10, 20, 30, 40]}
param_group_2 = {'subsample': np.linspace(0.1, 1, 5), 
                 'colsample_bytree': np.linspace(0.1, 1, 5), 
                 'colsample_bylevel': np.linspace(0.1, 1, 5)}
param_group_3 = {'alpha': np.logspace(-6, 3, 4), 'gamma': np.linspace(1, 9, 5)}
param_group_4 = {'scale_pos_weight': [0.5, 1, 2, 5, 10, 20, 50, 100, 500, 1000]}
param_group_5 = {'learning_rate': np.logspace(-4, -2, 11)}

    Gridsearch for parameter group 1: max_depth and min_child_weight

    We update the cur_params before performing the hyperparameter search. Also, it's a good practice to save the grid search results to minimize the chances of data loss. We use .to_pickle() method of pandas to save the resulting DataFrame. 

    search_params = param_group_1
cur_params.update(search_params)
pprint(cur_params)
        {'alpha': 1,
     'colsample_bylevel': 1,
     'colsample_bytree': 1,
     'gamma': 1,
     'learning_rate': 0.002,
     'max_depth': [3, 4],
     'min_child_weight': [1, 10, 20, 30, 40],
     'scale_pos_weight': 1,
     'subsample': 1}
    tmp_df, evals = cv_search_params(X_train, y_train, cur_params, all_features, rskf)
tmp_df.to_pickle('hyperparams_round1.pkl')
       Grid search on:

{'alpha': 1,
 'colsample_bylevel': 1,
 'colsample_bytree': 1,
 'gamma': 1,
 'learning_rate': 0.002,
 'max_depth': [3, 4],
 'min_child_weight': [1, 10, 20, 30, 40],
 'scale_pos_weight': 1,
 'subsample': 1}

started at 2021-06-04 12:41:46.384232
Total number of hyperparameter candidates = 10

CV 1 on:

{'max_depth': 3, 'min_child_weight': 1}

 started!

 Repeat 1, Fold 1 - PR-AUC tr = 0.816, PR-AUC vl = 0.752 (diff = 0.0639)
best number of boosting rounds tr = 386

 Repeat 1, Fold 2 - PR-AUC tr = 0.871, PR-AUC vl = 0.813 (diff = 0.0584)
best number of boosting rounds tr = 5289

 Repeat 1, Fold 3 - PR-AUC tr = 0.823, PR-AUC vl = 0.789 (diff = 0.0336)
best number of boosting rounds tr = 1209

...

Repeat 5, Fold 2 - PR-AUC tr = 0.762, PR-AUC vl = 0.739 (diff = 0.0232)
best number of boosting rounds tr = 1397

 Repeat 5, Fold 3 - PR-AUC tr = 0.708, PR-AUC vl = 0.742 (diff = -0.0342)
best number of boosting rounds tr = 838

 Repeat 5, Fold 4 - PR-AUC tr = 0.700, PR-AUC vl = 0.683 (diff = 0.0165)
best number of boosting rounds tr = 1110

Summary:
 mean PR-AUC training =  0.728
 mean PR-AUC validation = 0.718
 mean PR-AUC difference = 0.0094
CV 10 ended! (took 319.31 seconds)
Grid search ended at 2021-06-04 14:17:32.954835
​
    tmp_df
    current_params tr_avg tr_std val_avg val_std numtrees_avg numtrees_std diff time_taken
    0 {'max_depth': 3, 'min_child_weight': 1, 'subsa... 0.847 0.025 0.810 0.039 3163.150 1663.705 0.037 696.55
    1 {'max_depth': 3, 'min_child_weight': 10, 'subs... 0.848 0.018 0.816 0.032 4030.550 1415.623 0.032 857.18
    2 {'max_depth': 3, 'min_child_weight': 20, 'subs... 0.808 0.024 0.779 0.051 2194.450 1672.490 0.029 518.94
    3 {'max_depth': 3, 'min_child_weight': 30, 'subs... 0.784 0.017 0.767 0.040 1859.400 1292.788 0.017 452.01
    4 {'max_depth': 3, 'min_child_weight': 40, 'subs... 0.728 0.027 0.718 0.052 1168.550 277.548 0.009 319.31
    5 {'max_depth': 4, 'min_child_weight': 1, 'subsa... 0.874 0.042 0.817 0.037 3179.400 1812.708 0.057 783.87
    6 {'max_depth': 4, 'min_child_weight': 10, 'subs... 0.844 0.026 0.806 0.050 3240.800 1910.967 0.038 769.04
    7 {'max_depth': 4, 'min_child_weight': 20, 'subs... 0.810 0.025 0.780 0.051 2319.850 1727.073 0.030 574.93
    8 {'max_depth': 4, 'min_child_weight': 30, 'subs... 0.784 0.018 0.767 0.040 1858.900 1292.927 0.017 455.43
    9 {'max_depth': 4, 'min_child_weight': 40, 'subs... 0.728 0.027 0.718 0.052 1168.550 277.548 0.009 319.31

    We can remove the rows where the difference between the training and validation performance is significant. I take the threshold for this difference to be 2%, meaning that we disregard the parameters that cause a difference in performance $>2\%$ between training and validation sets. For the rest of this project, we will refer to this threshold as the acceptance threshold (not to be confused with the precision-recall threshold) and to this condition as the acceptance condition. This reduces the chances that the final model parameters cause overfitting. At the same time, we sort the output by val_avg which is the mean PR-AUC over the validation sets. 

    acceptance_threshold=0.02
cur_params = param_df[param_df['diff']<acceptance_threshold] \
    .sort_values('val_avg', ascending=False)
    current_params tr_avg tr_std val_avg val_std numtrees_avg numtrees_std diff time_taken
    3 {'max_depth': 3, 'min_child_weight': 30, 'subs... 0.784 0.017 0.767 0.040 1859.400 1292.788 0.017 452.01
    8 {'max_depth': 4, 'min_child_weight': 30, 'subs... 0.784 0.018 0.767 0.040 1858.900 1292.927 0.017 455.43

    max_depth=3 and min_child_weight=30 gives a reasonable PR-AUC while ensuring that the model's performance on the test data remains close to that of the training data. Note that using max_depth=4 gives the same performance as max_depth=3 so we move forward with the latter to reduce the complexity of the model. Next, we examine the second hyperparameter group.

    Acceptance threshold in the context of bias-variance trade-off

    We can think of acceptance condition in the context of bias-variance trade-off.

    We say a model has a high bias if it fails to use all the data in the observations. Such model relies mostly on the general information without taking into account the specifics. In contrast, we say a model has a high variance if it over-use theinformation in the data, i.e., relies too much on the specific data that is being trained on. Such model usually fails to generalize what it has learnt and reproduce its high performance when predicting the outcome for new, unseen data.

    We can demonstrate this using an example relevant to our problem. The table below shows aucpr for two models I and II. When comparing the two models, model I exhibits a very high aucpr on the training data (low bias) but a significant difference in performance when tested on the test data (high variance); Model II on the other hand gives a comparatively lower aucpr on both the training and test data (high bias) but the model's performance on both datasets is quite similar (low variance)

    Model I Model II
    train test train test
    0.99 0.8 0.75 0.73
    Bias low high
    Variance high low

    high bias and high variance both lead to errors in model performance. Ideally we would want the model to have low bias (less error on training data) and low variance (less difference between the model performance between the train and testing data). Bias-variance trade-off is the sweet spot where the model performs between the errors introduced by the bias and the variance. In this project, I used acceptance condition to set a value for Bias-variance trade-off; however, depending on the business goal, one may use a totally different criteria to find the best model hyperparameters.

    Gridsearch for parameter group 2: colsample_bylevel, colsample_bytree, and subsample

    We update cur_params using the parameters obtained in previous step. 

    cur_params.update({'max_depth': 3, 'min_child_weight': 30})
search_params = param_group_2
cur_params.update(search_params)
pprint(cur_params)
    {'alpha': 1,
 'colsample_bylevel': array([0.1  , 0.325, 0.55 , 0.775, 1.   ]),
 'colsample_bytree': array([0.1  , 0.325, 0.55 , 0.775, 1.   ]),
 'gamma': 1,
 'learning_rate': 0.002,
 'max_depth': 3,
 'min_child_weight': 30,
 'scale_pos_weight': 1,
 'subsample': array([0.1  , 0.325, 0.55 , 0.775, 1.   ])}
    tmp_df, evals = cv_search_params(X_train, y_train, cur_params, all_features, rskf)
       Grid search started at 2021-05-24 10:48:53.507958
   Total number of hyperparameter candidates = 125
   
   CV 1 on:

{'subsample': 0.1, 'colsample_bylevel': 0.1, 'colsample_bytree': 0.1}

 started!

Summary:
   
   
  mean PR-AUC training =  0.211
  mean PR-AUC validation = 0.197
  mean PR-AUC difference = 0.014
  best number of boosting rounds = 703
 CV 1 ended! (took 191.91 seconds)

    ...
  
   CV 125 on:

{'subsample': 1.0, 'colsample_bylevel': 1.0, 'colsample_bytree': 1.0}

 started!

Summary:
 mean PR-AUC training =  0.784
 mean PR-AUC validation = 0.767
 mean PR-AUC difference = 0.0171
 best number of boosting rounds = 1859
CV 125 ended! (took 475.21 seconds)

   Grid search ended at 2021-05-24 12:27:25.227479
    tmp_df[tmp_df['diff']<acceptance_threshold].sort_values('val_avg', ascending=False)
    index current_params tr_avg tr_std val_avg val_std numtrees_avg numtrees_std diff time_taken
    124 {'max_depth': 3, 'min_child_weight': 30, 'subs... 0.784 0.017 0.767 0.033 1859.600 1409.712 0.016 475.21
    119 {'max_depth': 3, 'min_child_weight': 30, 'subs... 0.777 0.014 0.765 0.037 547.000 536.632 0.011 207.12
    123 {'max_depth': 3, 'min_child_weight': 30, 'subs... 0.775 0.010 0.761 0.039 214.250 229.384 0.014 146.70
    118 {'max_depth': 3, 'min_child_weight': 30, 'subs... 0.776 0.015 0.760 0.041 691.100 889.920 0.015 235.01
    114 {'max_depth': 3, 'min_child_weight': 30, 'subs... 0.777 0.016 0.760 0.045 1015.400 1382.065 0.017 292.21
    ... ... ... ... ... ... ... ... ... ...
    5 {'max_depth': 3, 'min_child_weight': 30, 'subs... 0.211 0.039 0.211 0.055 862.600 364.775 -0.000 215.35
    10 {'max_depth': 3, 'min_child_weight': 30, 'subs... 0.203 0.037 0.210 0.068 1018.400 510.480 -0.007 239.26
    1 {'max_depth': 3, 'min_child_weight': 30, 'subs... 0.211 0.052 0.197 0.062 703.450 378.373 0.014 191.28
    2 {'max_depth': 3, 'min_child_weight': 30, 'subs... 0.211 0.052 0.197 0.062 703.450 378.373 0.014 191.46
    0 {'max_depth': 3, 'min_child_weight': 30, 'subs... 0.211 0.052 0.197 0.062 703.450 378.373 0.014 191.91

    125 rows × 9 columns

    Note that all the hyperparameter candidates satisfy the acceptance condition. We can query the first 10 hyperparameters with the best average PR-AUC on the validation data using: 

    [list(map(tmp_df[tmp_df['diff']<acceptance_threshold] \
          .sort_values('val_avg', ascending=False)['current_params'] \
          .iloc[x] \
          .get,
         ['subsample', 'colsample_bytree', 'colsample_bylevel']
         )
     ) for x in range(10)
]
    [[1.0, 1.0, 1.0],
 [1.0, 0.775, 1.0],
 [1.0, 1.0, 0.775],
 [1.0, 0.775, 0.775],
 [1.0, 0.55, 1.0],
 [1.0, 1.0, 0.325],
 [1.0, 1.0, 0.55],
 [1.0, 0.775, 0.55],
 [1.0, 0.55, 0.775],
 [0.775, 1.0, 1.0]]

    The results suggest that colsample_bylevel doesn't influenece the accuracy of the predictions. We can take a look at the evolution of PR-AUC for colsample_bylevel=1 and different values of subsample and colsample_bytree in our grid-search space.

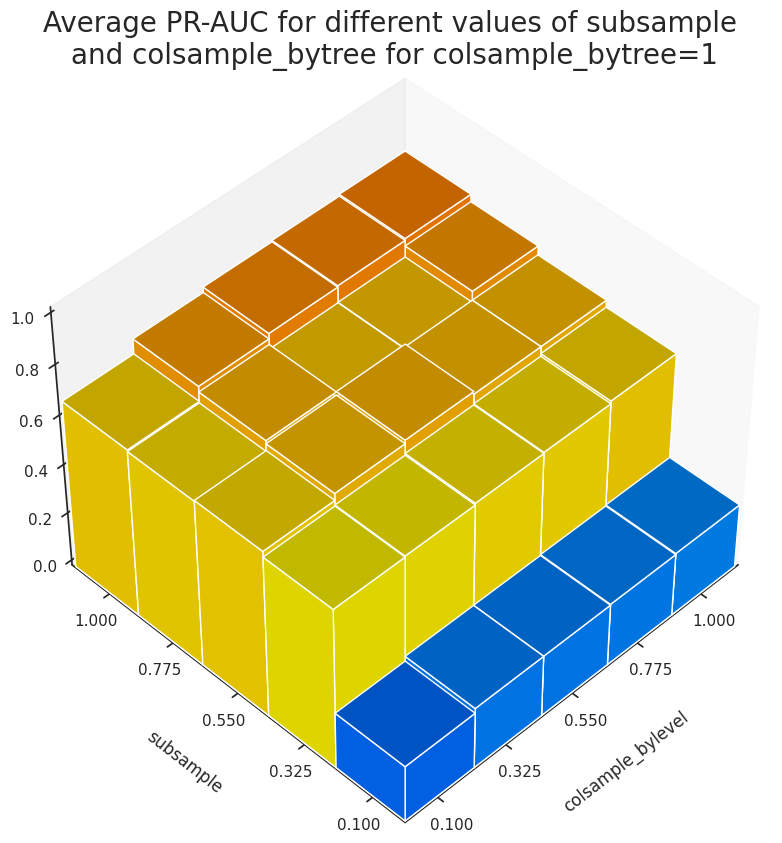
    Figure 3 shows that the variation of subsample has the most significant effect on the accuracy of the model.

    Finally, we set the first row of the resulting DataFrame as the initial hyperparameter for the next round of grid search. 

    cur_params = tmp_df[tmp_df['diff']<acceptance_threshold] \
                .sort_values('val_avg', ascending=False)['current_params'] \
                .iloc[0]
pprint(cur_params)
    {'alpha': 1, 
 'colsample_bylevel': 1.0, 
 'colsample_bytree': 1.0, 
 'gamma': 1, 
 'learning_rate': 0.002, 
 'max_depth': 3, 
 'min_child_weight': 30, 
 'scale_pos_weight': 1, 
 'subsample': 1.0}

    Gridsearch for parameter group 3: alpha and gamma

    cur_params.update(param_group_3)
pprint(cur_params)
    {'alpha': array([1.e-06, 1.e-03, 1.e+00, 1.e+03]),
 'colsample_bylevel': 1.0,
 'colsample_bytree': 1.0,
 'gamma': array([1., 3., 5., 7., 9.]),
 'learning_rate': 0.002,
 'max_depth': 3,
 'min_child_weight': 30,
 'scale_pos_weight': 1,
 'subsample': 1.0}
    tmp_df, evals = cv_search_params(X_train, y_train, cur_params, all_features, rskf)
tmp_df.to_pickle('hyperparams_round3.pkl')
    Grid search on:

{'alpha': array([1.e-06, 1.e-03, 1.e+00, 1.e+03]),
 'colsample_bylevel': 1.0,
 'colsample_bytree': 1.0,
 'eval_metric': 'aucpr',
 'gamma': array([1., 3., 5., 7., 9.]),
 'learning_rate': 0.002,
 'max_depth': 3,
 'min_child_weight': 30,
 'objective': 'binary:logistic',
 'scale_pos_weight': 1.0,
 'subsample': 1.0,
 'tree_method': 'gpu_hist'}

started at 2021-06-07 12:26:51.336554
Total number of hyperparameter candidates = 20

CV 1 on:

{'alpha': 1e-06, 'gamma': 1.0}

 started!

Summary:
 mean PR-AUC training =  0.781
 mean PR-AUC validation = 0.762
 mean PR-AUC difference = 0.0192
 average number of boosting rounds tr = 1450
CV 1 ended! (took 384.88 seconds)


    CV 20 on:

{'alpha': 1000.0, 'gamma': 9.0}

 started!

Summary:
 mean PR-AUC training =  0.672
 mean PR-AUC validation = 0.672
 mean PR-AUC difference = -0.0001
 average number of boosting rounds tr = 420
CV 20 ended! (took 168.19 seconds)

Grid search ended at 2021-06-07 14:34:06.880364

    tmp_df[tmp_df['diff']<acceptance_threshold] \
    .sort_values('val_avg', ascending=False) \
    .head()
    current_params tr_avg tr_std val_avg val_std numtrees_avg numtrees_std diff time_taken
    1 {'max_depth': 3, 'min_child_weight': 30, 'subs... 0.788 0.017 0.773 0.033 1999.550 1415.553 0.016 471.16
    6 {'max_depth': 3, 'min_child_weight': 30, 'subs... 0.788 0.017 0.773 0.033 2022.600 1409.712 0.016 474.74
    7 {'max_depth': 3, 'min_child_weight': 30, 'subs... 0.785 0.018 0.772 0.035 2003.700 1534.701 0.013 463.54
    2 {'max_depth': 3, 'min_child_weight': 30, 'subs... 0.784 0.017 0.772 0.034 1809.200 1205.948 0.013 432.78
    11 {'max_depth': 3, 'min_child_weight': 30, 'subs... 0.784 0.018 0.770 0.036 1929.900 1284.865 0.015 457.49

    At this point, the resulting optimal parameters achieve extremely close results in terms of the model performance metric. 

    [list(map(tmp_df[tmp_df['diff']<acceptance_threshold] \
          .sort_values('val_avg', ascending=False)['current_params'] \
          .iloc[x] \
          .get,
         ['alpha', 'gamma']
         )
     ) for x in range(5)
]
    [[1e-06, 3.0], [0.001, 3.0], [0.001, 5.0], [1e-06, 5.0], [1.0, 3.0]]

    When looking at val_avg for PR-AUC, the first two sets of hyperparameters in the table demonstrate the same performance, hence, we choose the one with larger alpha (=0.001) as it leads to a more conservative model. Because of the way we find the best number of boosting rounds when we use early stopping, one might question whether we use enuogh number of boosting rounds? I decided to run the same grid search as above, this time withough early stopping and also setting the maximum number of boosting rounds to 10000. In addition, we keep track of the variation of logloss and aucpr for the training and validation data with the number of boosting rounds. 

    tmp_df_no_early, evals = cv_search_params(X_train, y_train, cur_params, all_features, rskf, 
                                 eval_metric=['logloss','aucpr'], 
                                 num_boost_rounds=10000, early_stop_rounds=None)
tmp_df_no_early.to_pickle(f'hyperparam3_10000.pkl')
with open(f'hyperparam3_10000_evals.pkl', 'wb') as pickle_file:
    pickle.dump(evals, pickle_file)
          Grid search on:

{'alpha': array([1.e-06, 1.e-03, 1.e+00, 1.e+03]),
 'colsample_bylevel': 1,
 'colsample_bytree': 1,
 'gamma': array([1., 3., 5., 7., 9.]),
 'learning_rate': 0.002,
 'max_depth': 3,
 'min_child_weight': 30,
 'scale_pos_weight': 1,
 'subsample': 1}

started at 2021-06-09 05:23:46.155894
Total number of hyperparameter candidates = 20

CV 1 on:

{'alpha': 1e-09, 'gamma': 1.0}

 started!

Summary:
 mean PR-AUC training =  0.815
 mean PR-AUC validation = 0.789
 mean PR-AUC difference = 0.0258
CV 1 ended! (took 1753.62 seconds)

    CV 20 on:

{'alpha': 1.0, 'gamma': 9.0}

 started!

Summary:
 mean PR-AUC training =  0.800
 mean PR-AUC validation = 0.775
 mean PR-AUC difference = 0.0244
CV 20 ended! (took 1520.48 seconds)

Grid search ended at 2021-06-09 16:10:16.820294
    Variation of logloss and PR-AUC for alpha=0.001 and different values of gamma

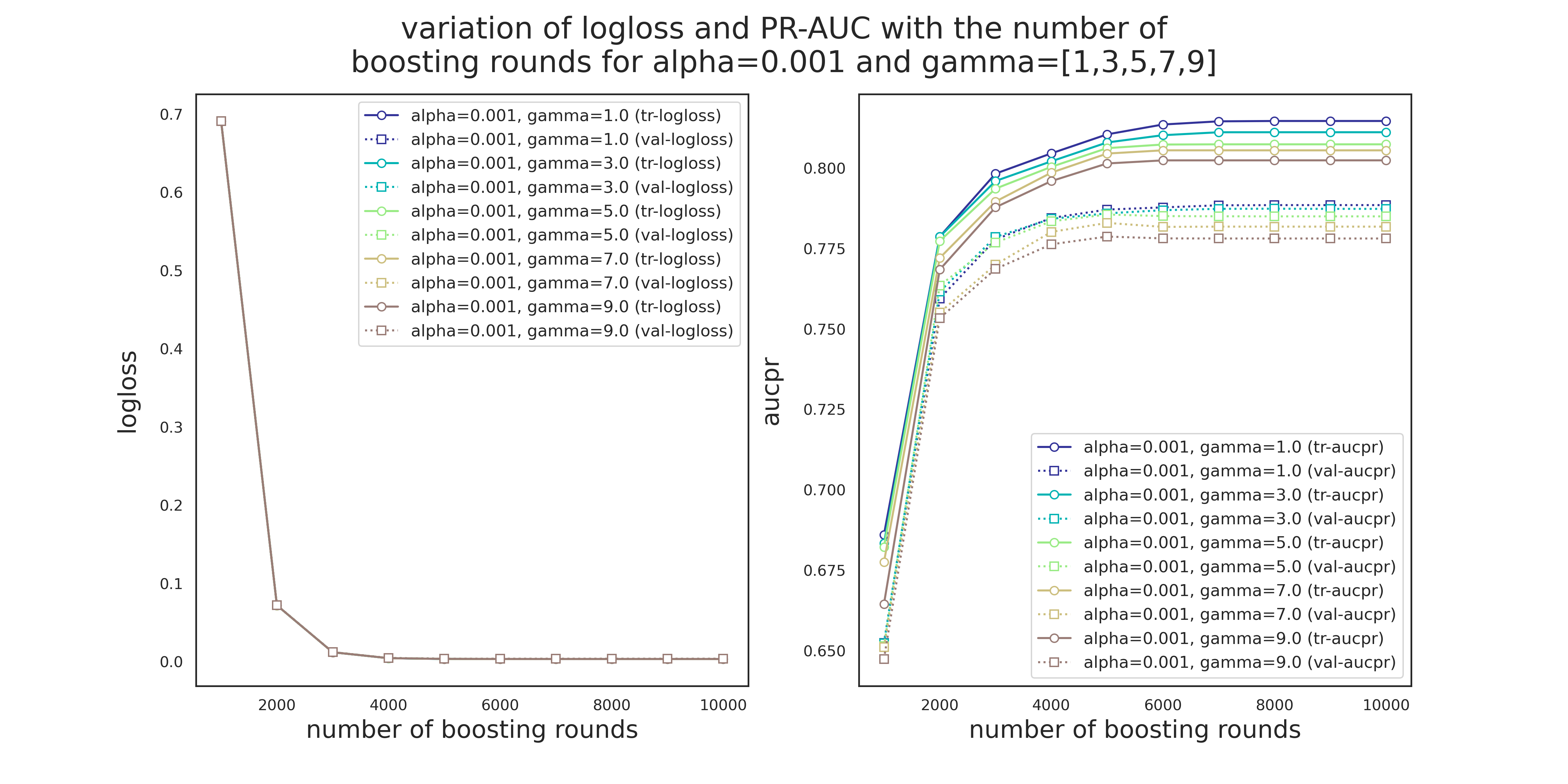
    Variation of logloss and PR-AUC for gamma=3 and different values of alpha

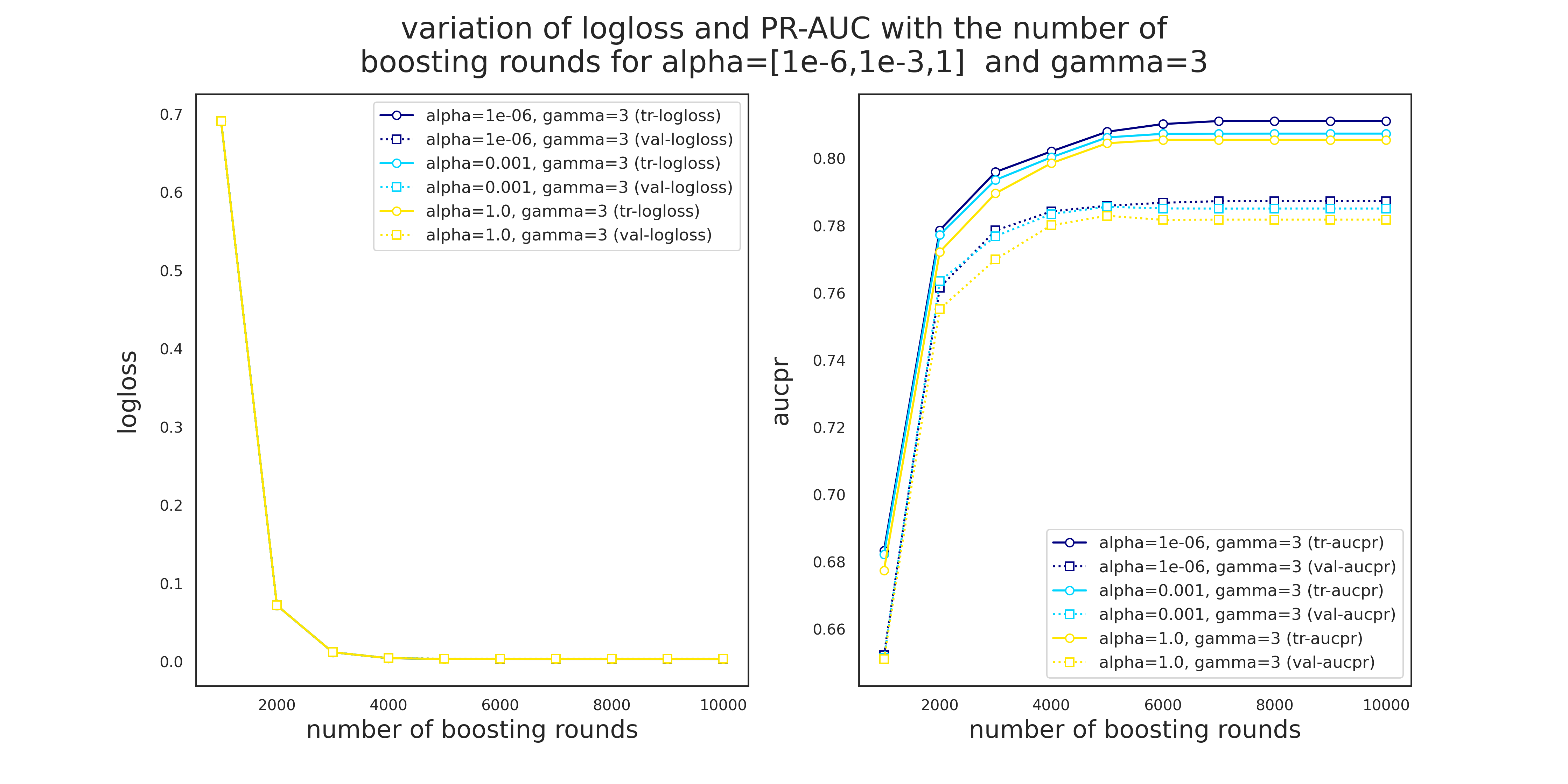
    There are a few observations to make from Figures 4 and 5.

    • Unlike Pr-AUC, Logloss is insensitive to the variation of alpha and gamma. This is most likely due to the severe imbalance of the classes. While PR-AUC is sensitive to imbalance, logloss is about the model's confidence in predicting the correct class, be it positive or negative.
    • Validation PR-AUC reaches its peak somewhere around 5000 trees followed by a slight reduction and then it plateaus. Train PR-AUC on the other hand is strictly increasing. This causes the gap between the training and validation PR-AUC to increase, i.e., overitting.
    • Model is more sensitive to the variation of gamma than alpha.
    • 5000 seems to be a safe maximum for the number of boosting rounds.
    We move on with gamma=3 and alpha=1e-3 to the next round of grid search. 

    cur_params = tmp_df[tmp_df['diff']<threshold].sort_values('val_avg', ascending=False)['current_params'].iloc[1]

    Gridsearch for parameter group 4: scale_pos_weight

    scale_pos_weight controls the balance of positive and negative weights which is specifically useful when dealing with highly imbalanced cases. A typical value to consider is sum(negative instances)/sum(positive instances), i.e.

    $$ \frac{\text{The number of observations with }\textbf{valid}\text{ transactions}}{\text{The number of observations with }\textbf{fraudulent}\text{ transactions}} $$ 
    from collections import Counter
counter = Counter(df['Class'])
print(f'Class distribution of the response variable: {counter}')
print(f'Majority and minority classes correspond to {100*counter[0]/(counter[0]+counter[1]):.3f}% ', 
      f'and {100*counter[1]/(counter[0]+counter[1]):.3f}% of the data, respectvively,', 
      f'\nwith positive-to-negative-ratio = {counter[0]/counter[1]:.1f}')
    Class distribution of the response variable: Counter({0: 284315, 1: 492})
Majority and minority classes correspond to 99.827%  and 0.173% of the data, respectvively, 
with positive-to-negative-ratio = 577.9

    Therefore, we make sure that this ratio or a value close to it is included in our hyperparameter candidates for scale_pos_weight. 

    pprint(cur_params)
    {'alpha': 0.001,
 'colsample_bylevel': 1,
 'colsample_bytree': 1,
 'eval_metric': 'aucpr',
 'gamma': 3,
 'learning_rate': 0.002,
 'max_depth': 3,
 'min_child_weight': 30,
 'objective': 'binary:logistic',
 'scale_pos_weight': 1,
 'subsample': 1,
 'tree_method': 'gpu_hist'}

    Note: the only reason to include scale_pos_weight=0.5 in the parameter search is to observe the model behavior. 

    search_params = param_group_4
cur_params.update(search_params)
pprint(cur_params)
    {'alpha': 0.001,
 'colsample_bylevel': 1,
 'colsample_bytree': 1,
 'gamma': 3,
 'learning_rate': 0.002,
 'max_depth': 3,
 'min_child_weight': 30,
 'scale_pos_weight': [0.5, 1, 2, 5, 10, 20, 50, 100, 500 ,1000],
 'subsample': 1}
    tmp_df, evals = cv_search_params(X_train, y_train, cur_params, all_features, rskf)
tmp_df.to_pickle('hyperparams_round4.pkl')
     Grid search started at 2021-05-31 14:23:33.726916
Total number of hyperparameter candidates = 10

CV 1 on:

{'scale_pos_weight': 0.5}

 started!

Summary:
 mean PR-AUC training =  0.729
 mean PR-AUC validation = 0.710
 mean PR-AUC difference = 0.0191
CV 1 ended! (took 178.08 seconds)

    CV 10 on:

{'scale_pos_weight': }

 started!

Summary:
 mean PR-AUC training =  0.759
 mean PR-AUC validation = 0.722
 mean PR-AUC difference = 0.0361
 
CV 10 ended! (took 448.14 seconds)

Grid search ended at 2021-05-31 15:21:49.174025
    tmp_df[tmp_df['diff']<acceptance_threshold] \
    .sort_values('val_avg', ascending=False) \
    .head()
    current_params tr_avg tr_std val_avg val_std numtrees_avg numtrees_std diff time_taken
    1 {'max_depth': 3, 'min_child_weight': 30, 'subs... 0.777 0.014 0.765 0.037 307.913 301.897 0.011 0:03:26
    0 {'max_depth': 3, 'min_child_weight': 30, 'subs... 0.702 0.013 0.690 0.048 91.575 169.184 0.012 0:02:14

    Note that only two of the search candidates for scale_pos_weight satisfy the acceptance condition. 

    [x['scale_pos_weight'] for x in tmp_df[tmp_df['diff']<acceptance_threshold] \
    ['current_params']]
    [0.5, 1]

    This is surprising because we expected a value close to sum(negative instances)/sum(positive instances) giving the best model performance. Looking at the variation of evaluation metric with might give us a hint about what might have gone wrong. Plotting the evolution of eval_metric with scale_pos_weight may reveal some more details regarding this discrepancy.

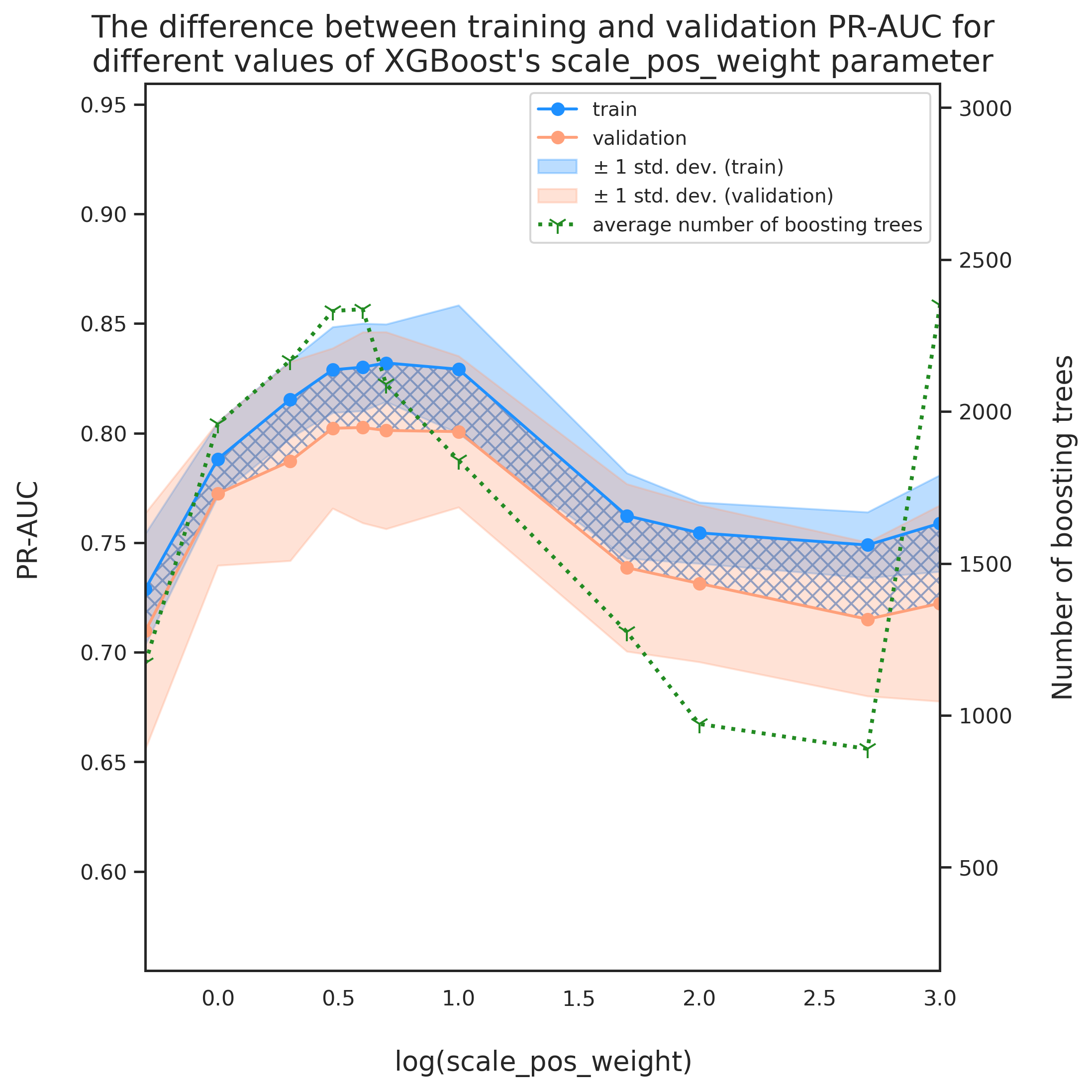
    Looking at Figure 6 above, we note that the scale_pos_weight values 10 an. We also observe that the deviation between the model performance on training versus validation data increases with the increase in scale_pos_weight. The increase in the width of the hatched region shows this deviation and we can see that for $\log(\mathrm{scale\_pos\_weight})\geq1$ the model is starting to overfit. The fact that the model does not demonstrate its best performance at XGBoost's recommended value should not be too concerning as these are general recommendations which can change with the imbalance ratio, the nature of data, the train-to-validation ratio, etc. Finally, we can see that there might be a scale_pos_weight value bigger than $1$ that demonstrates a better performance than scale_pos_weight=1 while satisfying the acceptance condition. We can explore this by performing another round of parameter search over a much smaller window as below. 

    param_group_4_new = {'scale_pos_weight': np.linspace(1,2,6)}
search_params = param_group_4_new
cur_params.update(search_params)
pprint(cur_params)
    {'alpha': 0.001,
 'colsample_bylevel': 1,
 'colsample_bytree': 1,
 'gamma': 3,
 'learning_rate': 0.002,
 'max_depth': 3,
 'min_child_weight': 30,
 'scale_pos_weight': array([1. , 1.2, 1.4, 1.6, 1.8, 2.]),
 'subsample': 1}
    tmp_df, evals = cv_search_params(X_train, y_train, cur_params, all_features, rskf)
tmp_df.to_pickle('hyperparams_round4_new.pkl')
    Grid search on:

{'alpha': 0.001,
 'colsample_bylevel': 1,
 'colsample_bytree': 1,
 'gamma': 3,
 'learning_rate': 0.002,
 'max_depth': 3,
 'min_child_weight': 30,
 'scale_pos_weight': array([1.0, 1.2, 1.4, 1.6, 1.8, 2.0]),
 'subsample': 1}

started at 2021-06-07 15:07:46.962607
Total number of hyperparameter candidates = 6

CV 1 on:

{'scale_pos_weight': 1.0}

 started!

Summary:
 mean PR-AUC training =  0.788
 mean PR-AUC validation = 0.772
 mean PR-AUC difference = 0.0167
 average number of boosting rounds tr = 1958
CV 1 ended! (took 260.34 seconds)

    CV 6 on:

{'scale_pos_weight': 2.0}

 started!

Summary:
 mean PR-AUC training =  0.815
 mean PR-AUC validation = 0.787
 mean PR-AUC difference = 0.0282
 average number of boosting rounds tr = 2168
CV 6 ended! (took 312.25 seconds)

Grid search ended at 2021-06-07 15:23:36.177770

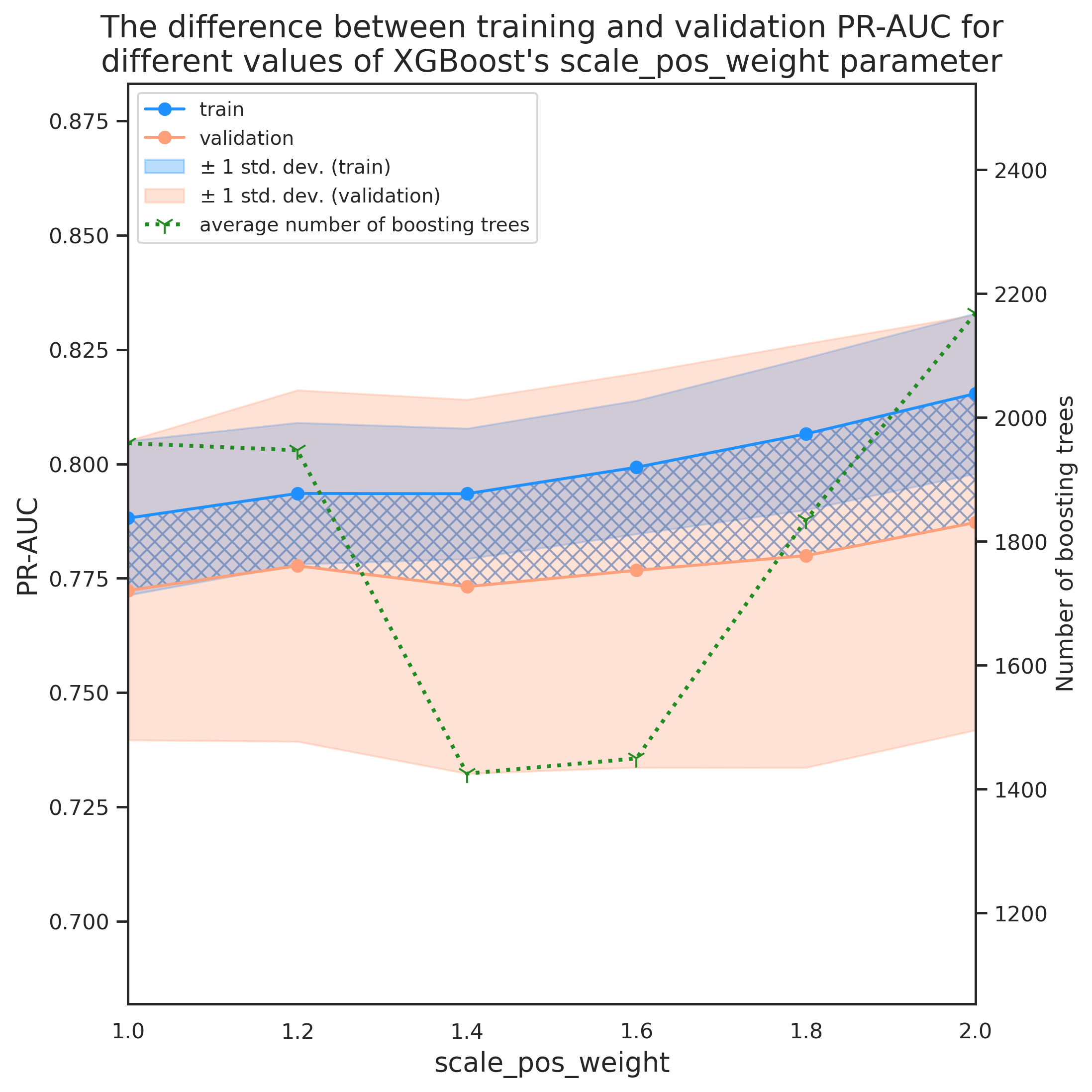
    tmp_df[tmp_df['diff']<acceptance_threshold] \
    .sort_values('val_avg', ascending=False) \
    .head()
    current_params tr_avg tr_std val_avg val_std numtrees_avg numtrees_std diff time_taken
    1 {'max_depth': 3, 'min_child_weight': 30, 'subs... 0.794 0.016 0.778 0.038 1958.311 1139.170 0.016 258.66
    0 {'max_depth': 3, 'min_child_weight': 30, 'subs... 0.788 0.016 0.772 0.037 1947.413 1279.757 0.011 260.34 
    tmp_df[tmp_df['diff']<acceptance_threshold] \
    .sort_values('val_avg', ascending=False) \
    .iloc[0]['current_params']['scale_pos_weight']
    1.2

    Note how this little change of scale_pos_weight from 1 to 1.2 improves the validation PR-AUC by roughly 1$\%$. This shows how important this hyperparameter is especially when dealing with highly imbalanced datasets.

    Important note regarding overfitting and the acceptance threshold

    Looking at the figure above, one might ask why we limited ourselves to acceptance condition? For instance, taking scale_pos_weight to be 3 rather than 1.2 increases the average train and validation PR-AUC by roughly 4$\%$ while the difference between the two is only about 0.7$\%$ above the acceptance threshold. This is a great question and in fact, some would characterize over fitting as a situation where increasing the complexity of the model slightly tends to increase the validation error, e.g. $\log(\mathrm{scale\_pos\_weight})>1$ in Figure6. There is no good answer to questions like this as the answer might change depending on the business objectives, computational resources, etc. The important thing here is to make sure that we understand the reasoning behind eliminating or accepting some candidates. I performed a similar analysis to previous round of grid search by repeating the grid search for scale_pos_weight with no early stopping.

    Variation of logloss and PR-AUC for scale_pos_weight=[1,5,20,100,1000]

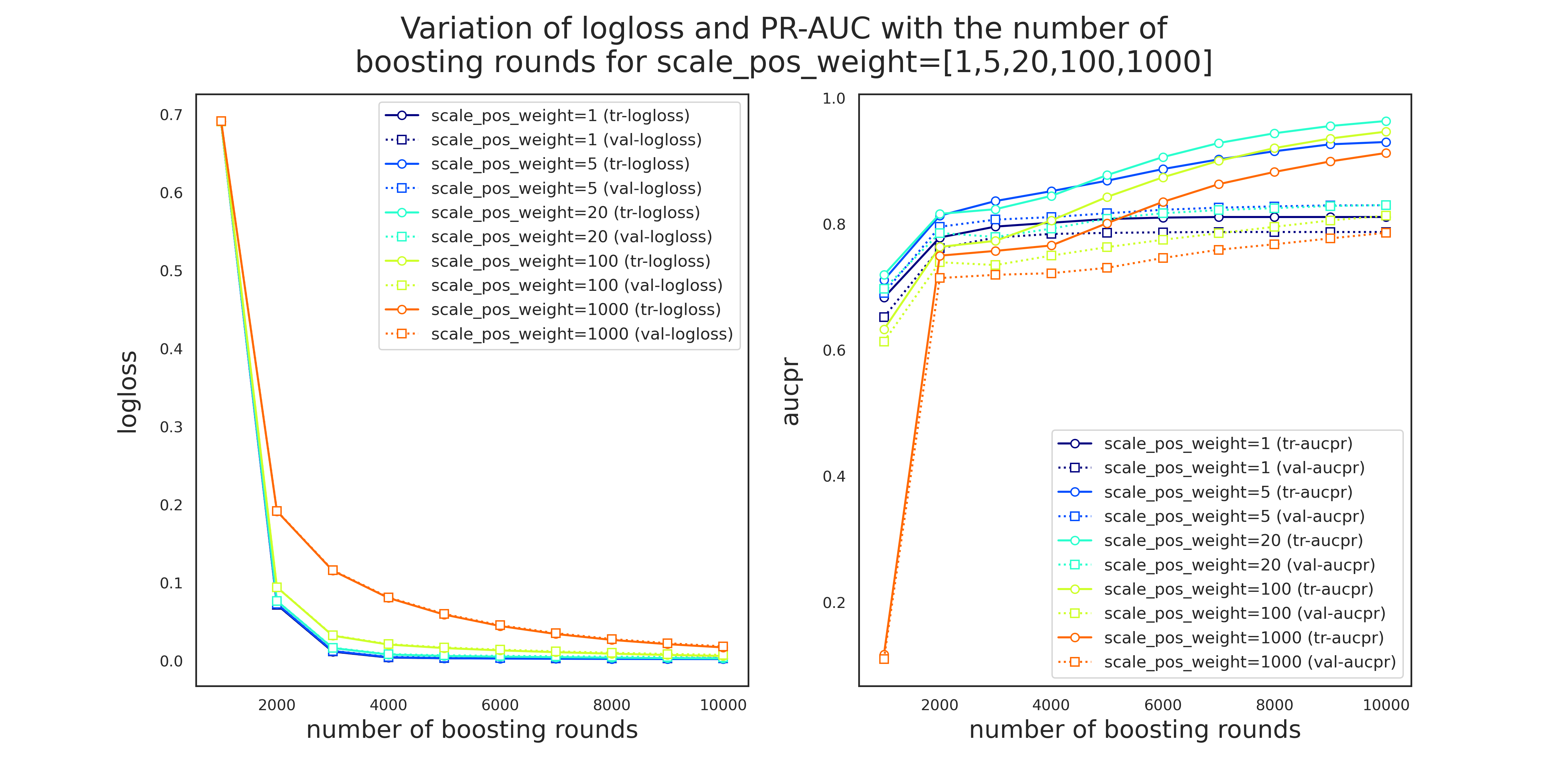
    • Notice that the reduction in logloss slows down for the higher values of scale_pos_weight. I believe that the possible reson behind this behavior is the model up samples the fraudulent class, i.e., repeats the positive instances scale_pos_weight times to make it a balanced problem but since the positive class is generally harder to predict, it requires a higher number of boosting rounds for the logloss to reduce.
    • Note that until around 2000 boosting rounds, the training and validation PR-AUC improve simultaneously and roughly with the same rate. In this period, scale_pos_weight=5 demonstrates a superior performance compared to other values.

    Nevertheless, we stick to the rule that we initially defined and move forward with scale_pos_weight=1.2.

    Gridsearch for parameter group 5: learning_rate

    The last step in our hyperparameter grid search is tuning the learning rate where we explore 11 learning rates in the range (0.0001, 0.01). Furthermore, to study the effect of Early_Stop_Rounds in more detail, we repeat the grid search for multiple values of Early_Stop_Rounds. This can help us to understand the benefits and potential disadvantages of using Early_Stop_Rounds. We also keep track of 'error' in addition to aucpr and logloss to see if we can get more insights about the evolution of eval_metrics with the grid search parameter. Finally, we increase the maximum number of boosting rounds to 10000. 

    cur_params.update({'scale_pos_weight': 1.2})
search_params = param_group_5
cur_params.update(search_params)
pprint(cur_params)
      {'alpha': 0.001,
 'colsample_bylevel': 1,
 'colsample_bytree': 1,
 'gamma': 3,
 'learning_rate': array([0.0001 , 0.00015849, ..., 0.00630957, 0.01]),
 'max_depth': 3,
 'min_child_weight': 30,
 'scale_pos_weight': 1.2,
 'subsample': 1}
    Evolution of eval_metrics with the number of boosting rounds and learning_rate
    dfs = []
early_stoppng_values = [200, 400, 1000, 2000, 5000, 10000]
for i, es in enumerate(early_stoppng_values):
    tmp_df, evals = cv_search_params(X_train, y_train, cur_params, all_features, \
                                     rskf, eval_metric=['error','logloss','aucpr'], \
                                     num_boost_rounds=10000, early_stop_rounds=es)
    tmp_df['early_stop'] = es
    with open('hyperparam5_{es}_evals.pkl', 'wb') as pickle_file:
        pickle.dump(evals, pickle_file, protocol=4)
    tmp_df.to_pickle('hyperparam5_{es}_df.pkl')
    dfs.append(tmp_df)

    First, we look at the variation of average error, logloss, and aucpr for training and validation data when there is no early stopping.

    There are some interesting observations to point out in Figure 9

    • All evaluation metric for the higher learning rates, i.e., lr=1e-2, 3.98e-3, remain unchanged after $n_{\text{tree}}\approx3000$. This means adding more complexity to the model does not imprpove the performance of the model.
    • In contrast, when looking at the results for lr=2.5e-4, we notice that even at a much higher number of boosting rounds, the validation metrics are still improving.
    • For the really low values of learning rate, i.e., lr=1e-4, the model is certainly underfitting as all the evaluation metrics are still improving at $n_{\text{tree}}\approx10000$.
    • The higher the learning rate gets, the sooner the model starts to overfit. This can be seen by looking at the error and aucpr subplots in Figure 9 where for the highest learning rate (lr=0.01), the divergence between the training and validation data results start at the very beginning where $n_{\text{tree}}\approx250$.

    How Early Stopping influences the optimal learning_rate

    We now look at the way using Early Stopping affects the computation cost, the best learning rate accorading to the criteria discussed previously, and whether or not that might affect the accuracy of the model. Note that the size of markers in Figure 10 are scaled by the square-root of the time taken to train the model.

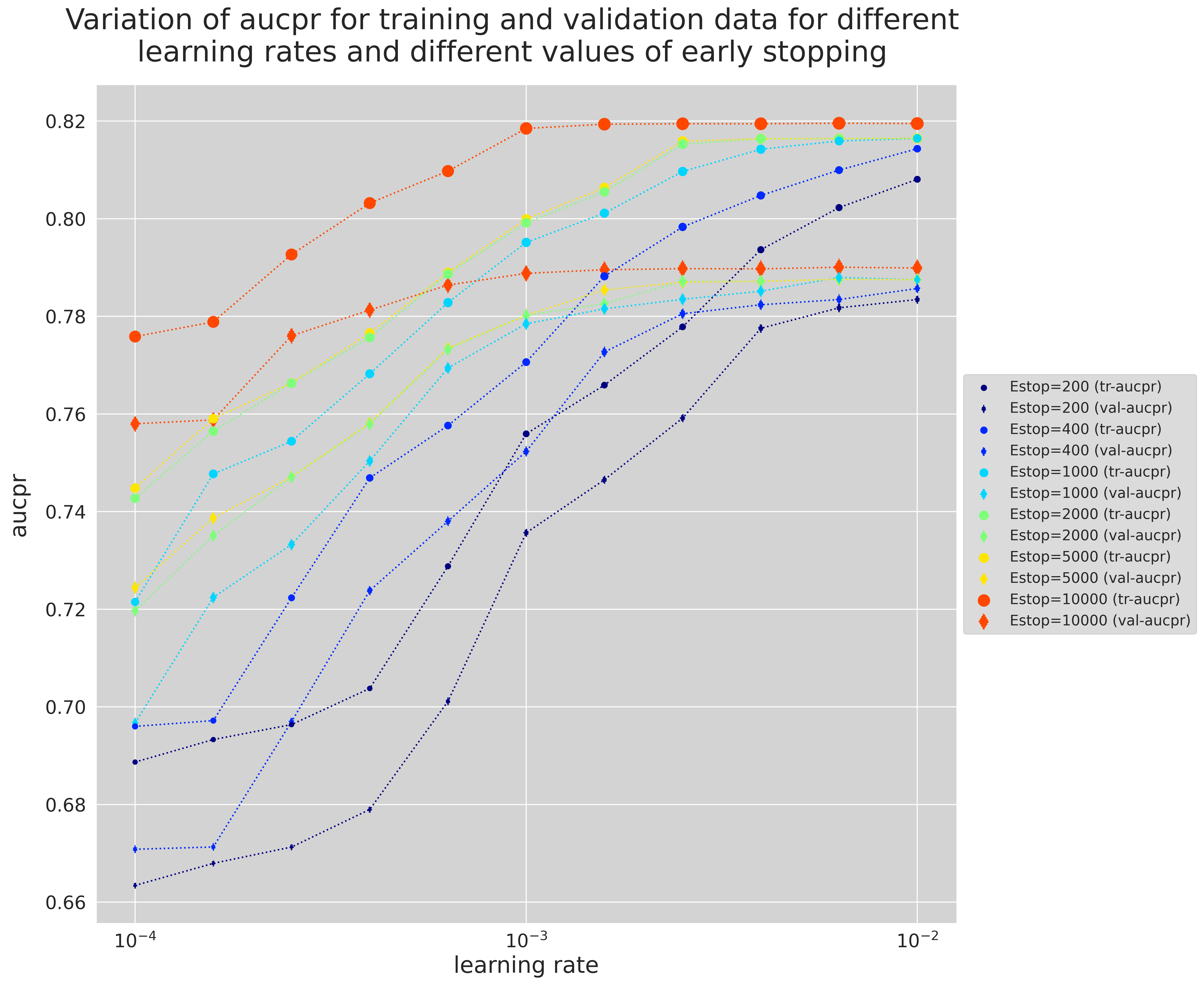
    Figure 10 shed light on choosing the best number of trees as the Early Stopping criteria.

    • The lower Early Stopping means the less computation cost. This can clearly be seen by the increase in the markers' size as the Early Stopping increases.
    • Notice that there is a bottleneck in all training-validation-pair curves for each Early Stop value where the training and validation aucpr are the closest. For instance for Estop=200, the bottleneck occurs at lr=2.5e-4 whereas for Estop=2000, it occurs at lr=6.51e-4.
    • Comparing the training and validation curves for (Estop=200, lr=2.51e-3) and (Estop=10000, lr=2.51e-4) with roughly the same performance for the training and validation PR-AUC. Notice that early stopping can significantly reduce the computation cost as the first case takes 107 seconds whereas the second case takes 1409 seconds. An almost 14 folds increase in the compuation cost.

    Finally, we can take a look at all the learning rates that meet the Acceptance Condition. 

    for i,es in enumerate(early_stoppng_values): 
    dfs[i]['early_stop'] = es
    dfs[i]['learning_rate'] = 0
    for j in range(len(dfs[i])):
        dfs[i]['learning_rate'].iloc[j]=f"{dfs[i]['current_params'].iloc[j]['learning_rate']:.2e}"
df_es = pd.concat(dfs, axis=0)
df_es = df_es[df_es['diff']<acceptance_threshold].sort_values('val_avg', ascending=False)
df_es = df_es.reset_index(drop=True)
df_es[['tr_avg','val_avg','time_taken','early_stop','learning_rate']].iloc[:,:10]
    tr_avg val_avg numtrees_avg time_taken early_stop learning_rate
    0 0.801 0.782 3227.400 438.81 1000 1.58e-03
    1 0.798 0.781 1963.000 285.39 400 2.51e-03
    2 0.800 0.780 5000.000 556.59 5000 1.00e-03
    3 0.799 0.780 4220.050 529.53 2000 1.00e-03
    4 0.795 0.778 3801.550 482.29 1000 1.00e-03
    5 0.794 0.778 985.150 138.15 200 3.98e-03
    6 0.793 0.776 10000.000 1409.15 10000 2.51e-04
    7 0.789 0.773 5000.000 551.06 5000 6.31e-04
    8 0.789 0.773 4322.450 539.58 2000 6.31e-04
    9 0.788 0.773 1848.850 263.90 400 1.58e-03

    Note that the value that we chose for Early Stopping gives the second best performance among all the combinations with only 0.1% lower accuracy than the best performance for val_avg. However, it takes rouhgly half the time that takes to train a model with (Estop=400, lr=2.51e-3) than the time that takes to train using (Estop=1000, lr=1.58e-3). We keep the early stopping value to be $400$ and move on to the last part of the project with lr=2.51e-3.

    Plotting the PR curves and finding the best threshold for the winner model

    In this part, we will find the threshold that gives the best balance of precision and recall. In addition, we plot the precision-recall curve for the training, validation, and test data. We could locate the threshold that gives the optimal balance between precision and recall using the Harmonic Mean of the two. Harmonic Mean or H-Mean of precision and recall is called F-measure or F-score which when optimized, will seek a balance between the precision and recall.

    $$ \text{F-score} = \frac{2 \times \text{Precision} \times \text{Recall}}{\text{Precision} + \text{Recall}} $$ or $$ \frac{1}{\text{F-score}} = \frac{1}{\dfrac{1}{2}\big(\dfrac{1}{\text{Precision}} + \dfrac{1}{\text{Recall}}\big)} $$

    One way to think about why optimizing F-score gives the best balance between precision and recall is that we can not get a high F-score if either one is very low. The threshold that gives the highest F-score is what we're looking for. First thing, we re-evaluate the model using the winner hyperparameters. This time, we also return the clf so that we can make predictions on the test data. Finally, we also need fold_preds so that we can plot the curves. 

    winner_params = {
    'max_depth': 3,
    'min_child_weight': 30,
    'subsample': 1,
    'colsample_bytree': 1,
    'colsample_bylevel': 1,
    'alpha': 1e-3,
    'gamma': 3,
    'scale_pos_weight': 1.2,
    'learning_rate': 2.51e-3,
}

final_eval_df, evals, fold_preds, clf = cv_summary(X_train, y_train, winner_params, all_features, rskf, 
                                                   eval_metric=['logloss','aucpr'], spit_out_fold_results=True,
                                                   num_boost_rounds=1963, early_stop_rounds=None, save_fold_preds=True)
     Repeat 1, Fold 1 - PR-AUC tr = 0.807, PR-AUC vl = 0.776 (diff = 0.0314)
 Repeat 1, Fold 2 - PR-AUC tr = 0.809, PR-AUC vl = 0.748 (diff = 0.0611)
 Repeat 1, Fold 3 - PR-AUC tr = 0.809, PR-AUC vl = 0.772 (diff = 0.0366)
 Repeat 1, Fold 4 - PR-AUC tr = 0.786, PR-AUC vl = 0.848 (diff = -0.0613)
 Repeat 2, Fold 1 - PR-AUC tr = 0.800, PR-AUC vl = 0.787 (diff = 0.0131)
 Repeat 2, Fold 2 - PR-AUC tr = 0.791, PR-AUC vl = 0.718 (diff = 0.0725)
 Repeat 2, Fold 3 - PR-AUC tr = 0.816, PR-AUC vl = 0.787 (diff = 0.0291)
 Repeat 2, Fold 4 - PR-AUC tr = 0.800, PR-AUC vl = 0.800 (diff = -0.0006)
 Repeat 3, Fold 1 - PR-AUC tr = 0.809, PR-AUC vl = 0.745 (diff = 0.0640)
 Repeat 3, Fold 2 - PR-AUC tr = 0.811, PR-AUC vl = 0.747 (diff = 0.0637)
 Repeat 3, Fold 3 - PR-AUC tr = 0.803, PR-AUC vl = 0.802 (diff = 0.0007)
 Repeat 3, Fold 4 - PR-AUC tr = 0.787, PR-AUC vl = 0.854 (diff = -0.0669)
 Repeat 4, Fold 1 - PR-AUC tr = 0.809, PR-AUC vl = 0.734 (diff = 0.0756)
 Repeat 4, Fold 2 - PR-AUC tr = 0.791, PR-AUC vl = 0.771 (diff = 0.0203)
 Repeat 4, Fold 3 - PR-AUC tr = 0.793, PR-AUC vl = 0.837 (diff = -0.0434)
 Repeat 4, Fold 4 - PR-AUC tr = 0.802, PR-AUC vl = 0.765 (diff = 0.0375)
 Repeat 5, Fold 1 - PR-AUC tr = 0.800, PR-AUC vl = 0.774 (diff = 0.0262)
 Repeat 5, Fold 2 - PR-AUC tr = 0.805, PR-AUC vl = 0.776 (diff = 0.0294)
 Repeat 5, Fold 3 - PR-AUC tr = 0.797, PR-AUC vl = 0.818 (diff = -0.0212)
 Repeat 5, Fold 4 - PR-AUC tr = 0.805, PR-AUC vl = 0.782 (diff = 0.0228)
Summary:
 mean PR-AUC training =  0.801
 mean PR-AUC validation = 0.782
 mean PR-AUC difference = 0.0195
    # making predictions on the train and test data
# Winner model parameters
param_dict = {'tree_method':'gpu_hist'
              'objective':'binary:logistic'
              'eval_metric':'aucpr'}
param_dict.update(winner_params)
# train data into xgb.DMatrix
xg_train = xgb.DMatrix(X_train, feature_names=all_features, label=y_train)
# train
clf = xgb.train(param_dict, xg_train, num_boost_round=1977)
# predict train
y_pred_train = clf.predict(xg_train)
# predict test
y_pred_test = clf.predict(xgb.DMatrix(X_test, feature_names=all_features))

# chnage key names and update with train and test predictions
fold_preds['cv-train'] = fold_preds.pop('train')
fold_preds['cv-val'] = fold_preds.pop('eval')
fold_preds['train'] = [[y_train, y_pred_train]]
fold_preds['test'] = [[y_test, y_pred_test]]

    Plotting the PR curves

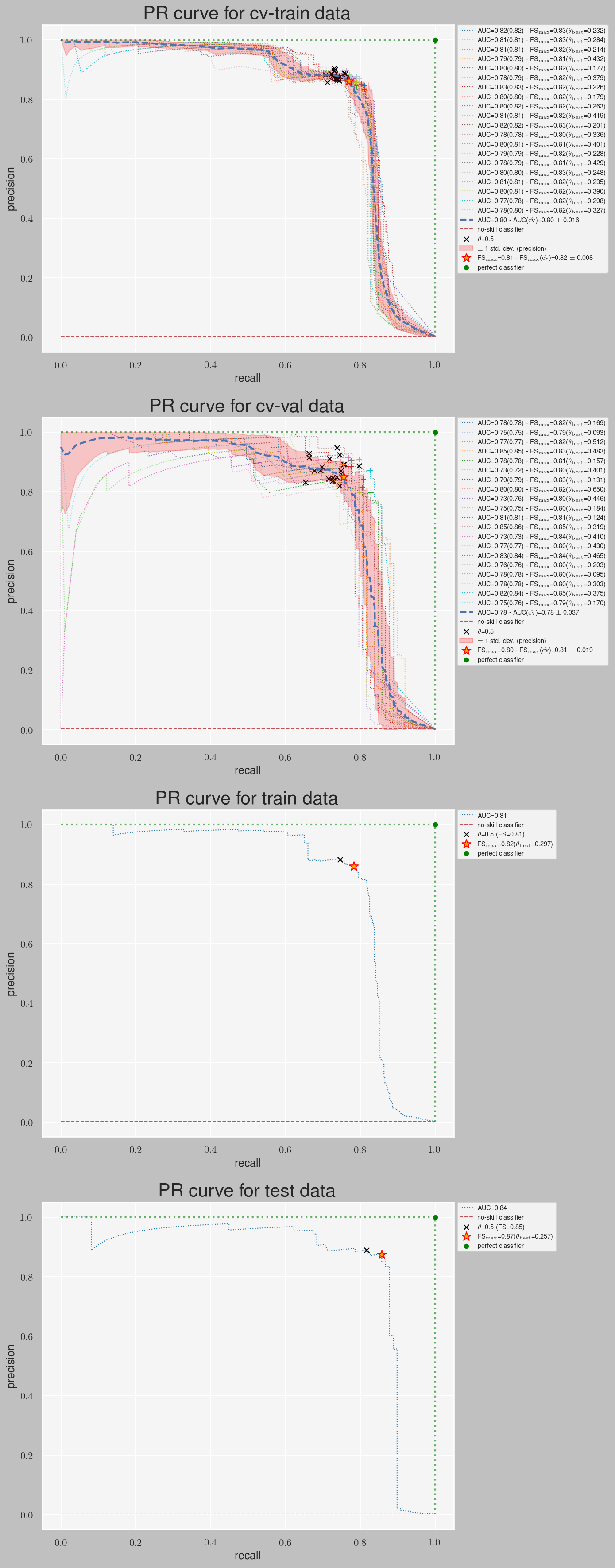
    Notes:

    • Figure 11 shows the precision-recall curve for cv-train, cv-val, train, and test, where cv denotes the plots of all the folds in cross-validation folds.
    • For cv curves, the mean PR curve is calculated by averaging over the folds. Because the number of data points in each fold and the corresponding PR curve is different, these curves are approximated using np.interp() so that they have the same shape and therefore could be averaged. Area1 and Area2 in cv plot legends AUC=Area1(Area2) denote the PR-AUC of the actual and approximated curves, respectively.
    • For cv curves, the average PR curve is shown using a thick, blue dashed line
    • Note that there's a negligible difference between the
      • AUC of the approximated curves and the actual curves
      • AUC($\hat{\mathrm{cv}}$) (average over cv AUCs) and the AUC of the mean PR curve
    • × and colored + (in cv plots) show the precision and recall calculated at $\theta=0.5$ and $\theta=\theta_{\mathrm{best}}$, respectively, where $\theta=\theta_{\mathrm{best}}$ is the threshold that maximizes the F-score. FS$_{\max}$ is the F-score calculated at $\theta=\theta_{\mathrm{best}}$.
    • By looking at the cv-val plot, we notice that in some folds, there's a significant drop in precision at threshold values close to 1 (top left). I reproduced those instances in the figure below:

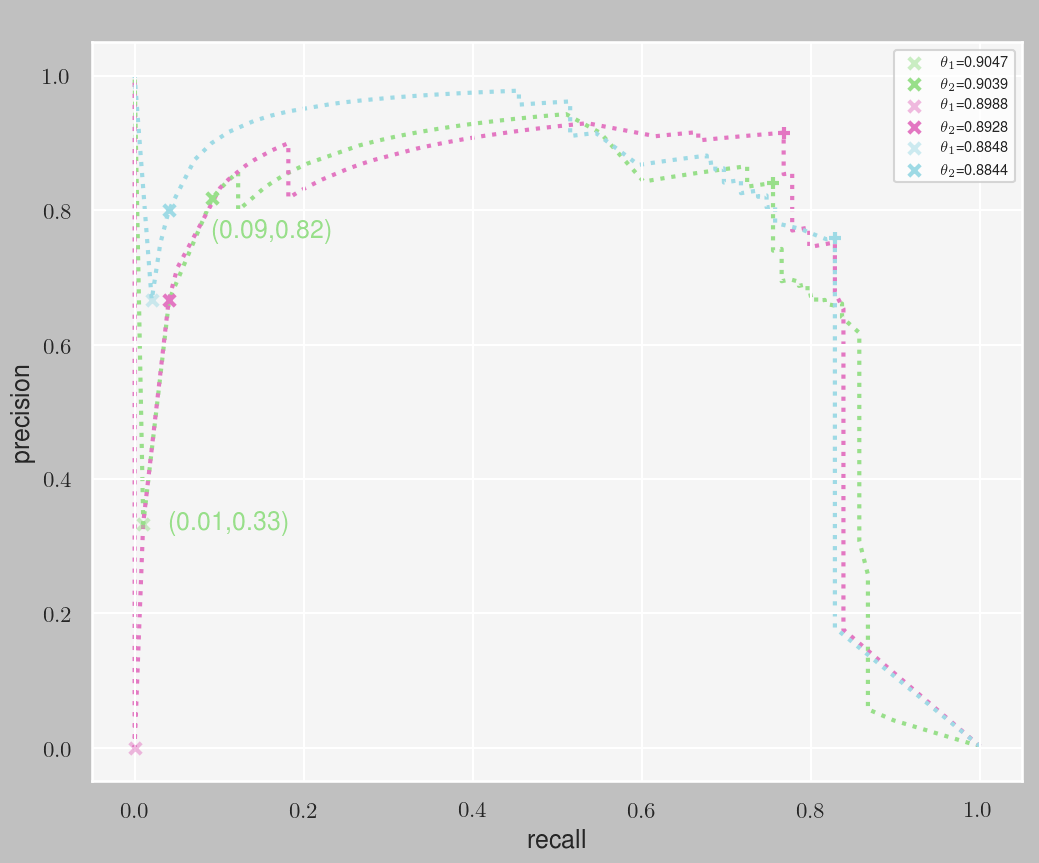
      Considering that the positive class includes that fraudulent transactions, this shows that the model is mistakenly classifying a lot of valid transactions as fraud ($\text{FP}$), causing the sudden drop in precision. This can mean that these specific folds contain a lot of observations from the positive class (fraud) that are hard to predict (close to the decision boundary).

      For the sake of clarity, let's focus on the green curve in Figure 12 where a slight decrease in threshold from $0.9047$ to $0.9039$ leads to an increase in (recall,precision) from (0.01,0.33) to (0.09,0.82). We can translate this into something even more clear; For every observation $X_i$, model prediction is a probability $p_i$ that measures the chance of $X_i$ belonging to the positive class, where $0 \leq p_i \leq 1$. What $\theta_1=0.9047$ means is that at this threshold, $X_i$ will be classified positive (fraud transaction) only if $p_i>0.9047$ and otherwise it will be classified as negative (valid transaction).

      $$ \begin{align} \text{Recall}&=\dfrac {\text{TP}}{\text{TP+FN}}\\[2ex] \text{Precision}&=\dfrac {\text{TP}}{\text{TP+FP}} \end{align} $$

      The fact that there are roughly 100 positive observations in each fold and the recall value $0.01$ at $\theta_1=0.9047$ means that of the $\approx$100 fraud observations, there's only one observaation that the model can classifiy as fraud with a probability higher than $0.9047$, i.e., $\text{TP}=1$. Noting that $\text{Precision}=0.33\approx \dfrac{1}{3}$, this means $\text{FP}=2$.

      Similarly, at the slightly lower threshold $\theta_1=0.9039$, the recall value $0.09$ means that with the new threshold, the model can correctly identify 9 fraud instances $X_j$ with $p_i>0.9039$ while the rest of the fraud observations $X_j$ will be classified as valid because $p_j\leq0.9039$. Noting that $\text{Precision}=0.82\approx \dfrac{9}{11}$, this means that $\text{FP}$ remains unchanged at 2.

    Comparison with the baseline model

    In this last part, we compare the performance of hypertuned model with that of the baseline model. First, let's take a look at the hyperparameter values of the two models:

    Parameter Baseline Model hypertuned Model
    n_estimator 100 1963
    max_depth 6 3
    min_child_weight 1 30
    subsample 1 1
    colsample_bytree 1 1
    colsample_bylevel 1 1
    alpha 0 1e-3
    gamma 1 3
    scale_pos_weight 1 1.2
    learning_rate 0.3 2.51e-3

    Notice that the biggest differences in parameter values are for n_estimators, max_depth, min_child_weight, and learning_rate. We first train and test the baseline model. Next, we apply the best thresholds that we obtained for the training and test data and save them while also saving them using the default threshold $\theta=0.5$. This can shed light on the importance of finding $\theta_{\mathrm{best}}$ that maximizes the F-score. Finally, we make comparisons with the winner model regarding the performance of the models where we use sklearn's classification_report and confusion_matrix as our tools. These comparisons can help us assess how well the winner model parameters generalize and categorize the unseen data.

    Training and testing the baseline model

    # Baseline model parameters
param_dict = {'tree_method':'gpu_hist'
              'objective':'binary:logistic'
              'eval_metric':'aucpr'}
# fit and predict baseline
baseline_XGBoost = xgb.XGBClassifier(**param_dict)
baseline_XGBoost.fit(X_train, y_train)
y_pred_train_baseline = baseline_XGBoost.predict(X_train)
y_pred_test_baseline = baseline_XGBoost.predict(X_test)

    Applying PR curve optial thresholds and isualizing the classification report

    First, let's measure aucpr: 

    preds = [y_pred_train, y_pred_test, 
         y_pred_train_50, y_pred_test_50,
         y_pred_train_baseline, y_pred_test_baseline]
trues = [y_train, y_test]
for i,pred in enumerate(preds):
    print(f"{average_precision_score(trues[i%2],pred):.2f}")
    0.81
0.84
0.66
0.73
1.00
0.81

    Next, we apply the best thresholds to the winner model predictions: 

    # threshold=0.5
y_pred_train_50 = np.round(y_pred_train)
y_pred_test_50 = np.round(y_pred_test)

# apply threshold

y_tr_pred[y_tr_pred<0.297]=0
y_tr_pred[y_tr_pred>=0.297]=1

y_test_pred[y_test_pred<0.257]=0
y_test_pred[y_test_pred>=0.257]=1

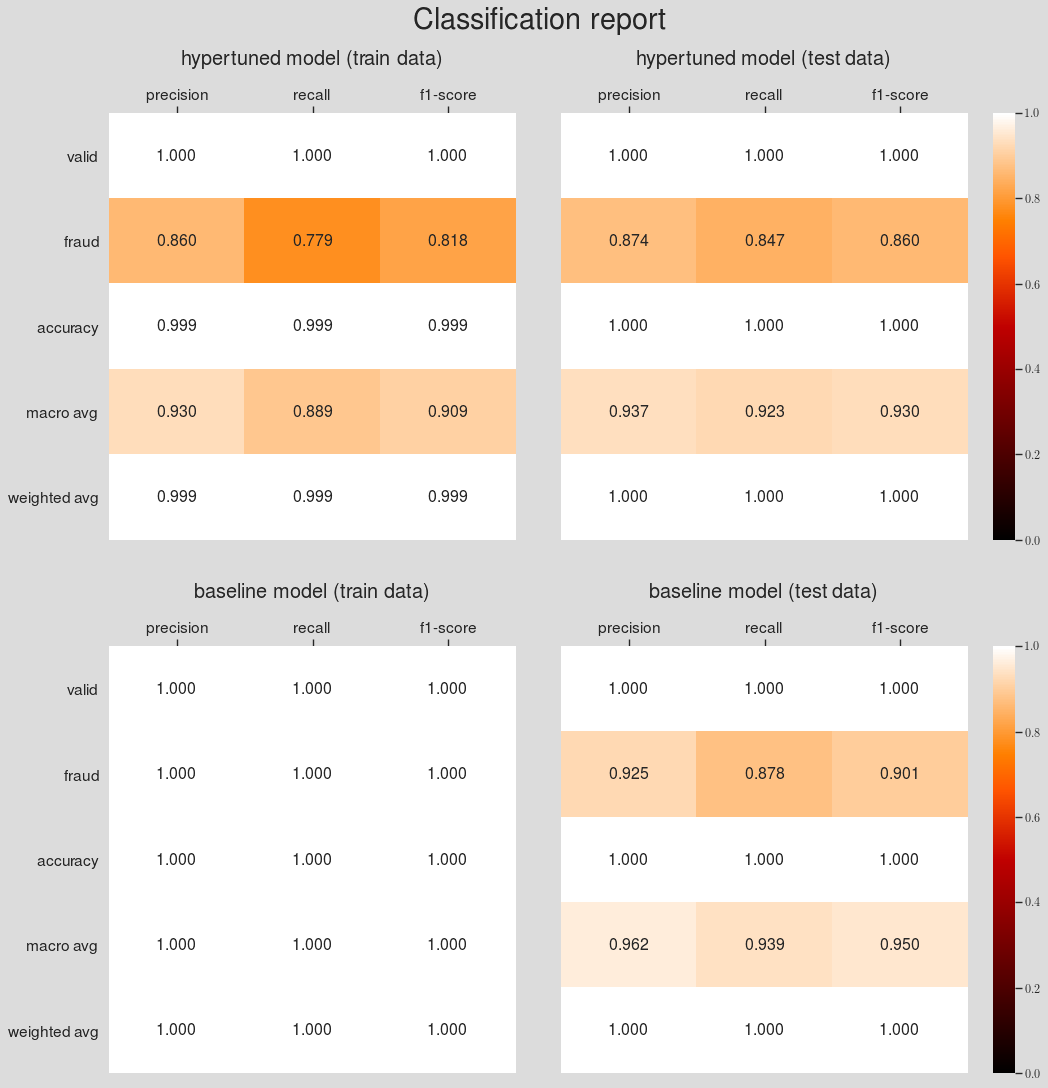
    Visualizing the confusion matrix for the baseline and winner model predictions (using $\theta=0.5$ and $\theta=\theta_{\mathrm{best}}$)

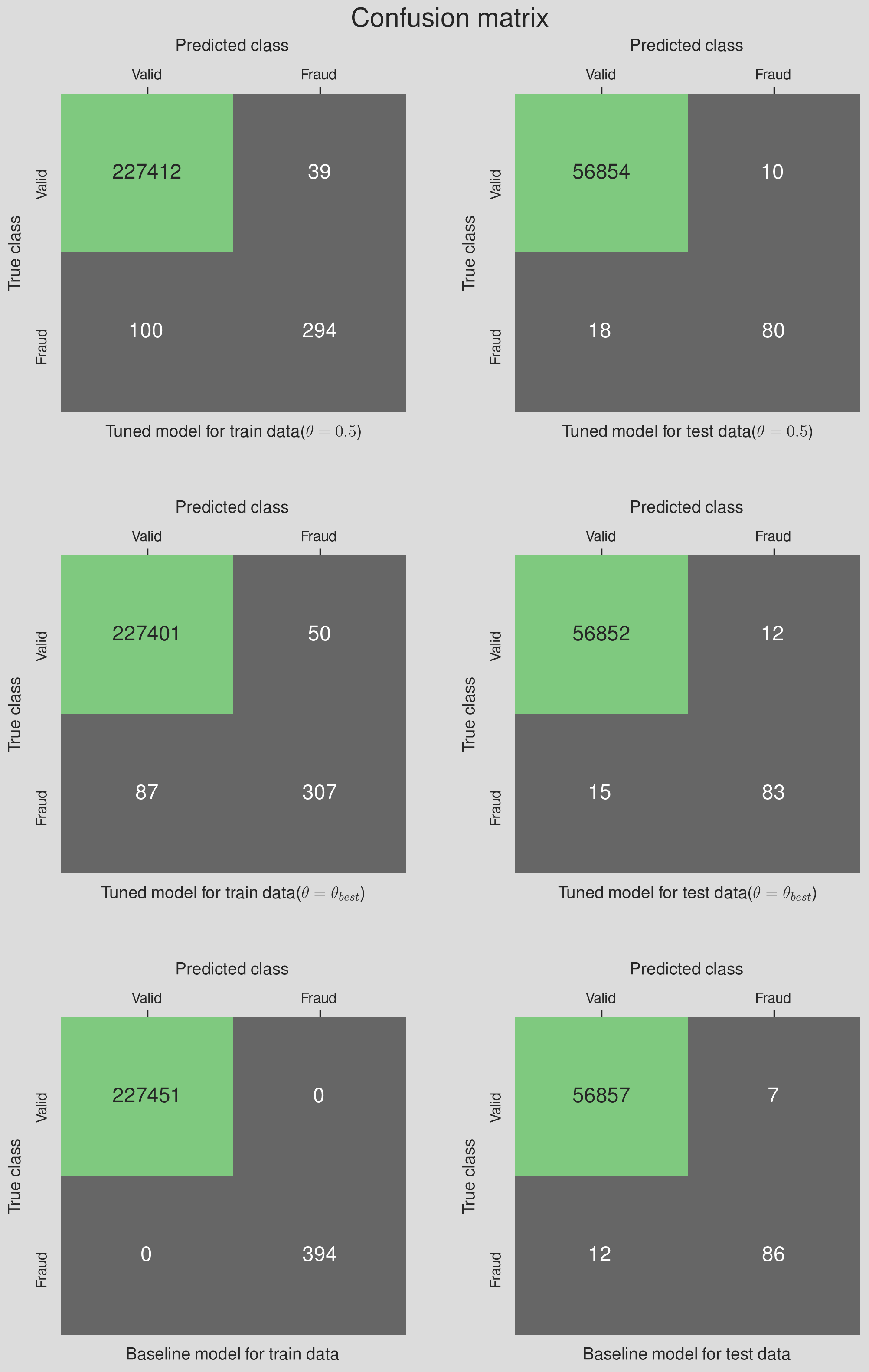
    Notes:

    • The baseline model is severly overfitting. This is evident in both Figures 13 and 14 when comparing the training and test results (aucpr train=1.00, aucpr train=0.81). In fact, according to the acceptance criteria, the baseline model needs to be discarded.
    • The hypertuned model with the optimal threshold has a lower Type II error (#False negative) compared to the model with $\theta=0.5$; This comes at the cost of a higher Type I error (#$\mathrm{FN}$). For the credit card data, however, one would naturally care much more about reducing the Type II error than the Type I error.
    • Depending on the business objective, the success/failure of the model can be phrased differently. For instance, if we consider the ability to detect all fraud transactions (regardless of some valid transactions labeled as fraud) we can say the hypertuned and baseline models were $84.7$% and $87.7$% successful, respectively. This success measure chnage to $99.806$% and $99.815$% if the business cares about the success in predicting valid transactions only. In real life scenarios, the model evaluation function is persumably more complicated than this. Realisticly, the business objective should be combination of
      • Minimizing the losses due to fraud transactions
      • Minimizing the model complexity
      • Minimizing the customer churn
      • Maximizing the business profit
      • Minimizing the Type II error
      • ...

    Summary and Conclusion

    • In this project, we went through the process of finding the best supervised model to identify fraudulent transactions in a credit card transaction data
    • The dataset was extremely imbalance with a valid-to-fraudulent class ratio of 581 to 1
    • Our analysis found the XGBClassifier() to be the model that best performs on this specific data set and assuming the PR-AUC to be the performance criteria.
    • Due to the large number of parameters that XGBoost takes, we employed a sequential grid search to find the optimal hyperparameters of the model.
    • The sequential search was performed in 5 steps where at each step, the optimal value for a single or a group of hyperparameters was obtained via cross validation.
    • We used RepeatedStratifiedKFold to reduce the error in the estimate of mean model performance.
    • We learned that early stoppping can benefits the training and tuning process by reducing the overfitting and reducing the computation cost.
    • We defined a $2%$ threshold as the maximum allowed difference between the train and validation PR-AUC. We did this so that we don't end up with a winner model that the train and test performances are significantly different(overfitting); however, one can set their criteria according to the business objective. For instance, if the business only cares about maximizing the recall (minimizing $\mathrm{FN}$), they set a threshold for the difference in performance between train and validation data in predicting recall instead of PR-AUC.
    • We were able to reduce the overfitting in the baseline model by conducting a sequntial grid search on the xgboost classfier model parameters relevant to the imbalanced classification problem.